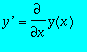Singular and General Solutions of Algebraic Differential Equations

Examples and their analysis with the diffalg package

Evelyne Hubert

Let be a multivariate polynomial over a field of characteristic zero. We write .

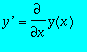A solution of the ordinary differential equation is said to be singular if it satisfies

This is the definition that prevails since the work of Darboux (1870) on the subject. It is nonetheless not equivalent to the original idea of Laplace (1772) and Lagarange (1774), for whom the singular solution of a first order differential equation is a solution that cannot be obtained by substituting a numerical value to the arbitrary constant of the general solution . This non-equivallence will be illustrated in a next section.

Clairaut (1734) seems to have been the first to come across the existence of singular solutions. In the equations, to which he has given his name, the singular solution is an enveloppe of the nonsingular solutions. We will illustrate that this need not to be the case. See also the introductory document :

"How to define the general and the singular solution of a differential equation?"
on http://www-sop.inria.fr/cafe/Evelyne.Hubert

We will give example of partial differential equations of first order to show that their singular solutions exhibit similar properties as the ones of first order differential equations, namely some enveloping and limiting property. These are the only two possibilities for first order. With the toboganning example, we shall show that these two cases can occur in a simple physical sytem according to the initial energy.

We will see, again with examples, the diversity of behaviour that appear in higher order differential equations.

In the section preparation polynomial and minimal decomposition, we introduce the tools to make a first classification of the singular solutions according to their properties. For a complete explanation of these tools, look at

E. Hubert, Essential component of a differential algebraic equation , Journal of Symbolic Computations (1999) volume 29 number 4-5 pages 657-680.

These tools are used on three examples. The Universal equation of Rubel, a Cahzy equation and the equation of the travelling wave of the KdV. In this latter we see how our tools can be used to determine the nature of the wave. The tools are implemented in Maple and embedded in the diffalg package, a package of differential algebra. See and download from:

http://daisy.uwaterloo.ca:80/~ehubert/Diffalg

> with(diffalg);

Clairaut's equation

Clairaut's work was concerned with geometry. He first brought out this paradox that , for certain differential equations, there exist solutions which are not embedded in the general solution - i.e. that cannot be obtained by specialising the arbitrary constants.

A class of differential equations is named after Clairaut. Clairaut gave the mean to determine the singular solutions of these equations. Now, these equations are recognized by the classification methods of standard computer algebra system solvers.

> ode := -y(t)+t*diff(y(t),t)-diff(y(t),t)^2;

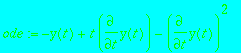
> dsolve(ode,y(t));

The general solution consists of straight lines while the singular solution is a parabola. It turns out that the singular solution is an envelope of the family of straight lines of the general solution.

> plot([t^2/4,seq(-(c/2)^2+c*t/2,c=-3..3)], t=-4..4, y=-2..3);

A general way to determine if there are any singular solutions to a differential equation is provided by these command of the diffalg package. it will also determine the equation of the singular solution.

> R := differential_ring(ranking=[y], derivations=[t], notation=diff):

> equations(Rosenfeld_Groebner([ode],R));

Arbitrary constants

Consider the following ordinary differential equations.

As unveiled by the diffalg[Rosenfeld_Groebner] command, it admits 2 singular solutions.

> ode := diff(y(t),t)^3-4*t*y(t)*diff(y(t),t)+8*y(t)^2;

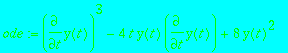
> R := differential_ring(ranking=[y], derivations=[t],notation=diff):

> S:=equations(Rosenfeld_Groebner([ode],R));

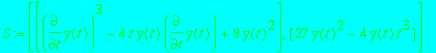
The singular solutions consist of a cubic and the zero function.

The solutions under closed form are:

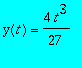
We see that, while the cubic cannot be obtained from the general solution, by specializing in the closed form of the general solution we obtain the second singular solution.

Note that both the cubic and the zero function are envelopes of the non-singular solution.

> d1:=plot(4*t^3/27,t=-5..5,y=-15..15, thickness=3):
d2:= plot({ seq((a/6)^3*(t-(a/6)^3)^2,a=-9..9)},t=-5..5,y=-15..15): plots[display]({d1,d2});

We could have a-priori, i.e. without previous knowledge of the closed form solution, unveiled the fact that the zero function was embedded in the general solution. This can be done through the following command of the diffalg package.

> M := equations(essential_components (ode, R));

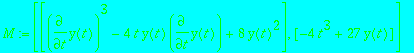
We have here a minimal description of the solution set of the ordinary differential equation under consideration.

Note that dsolve now uses diffalg to compute the singular solutions.

> dsolve(ode, y(t));

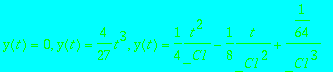
Envelope?

Consider the following ordinary differential equations. With diffalg[Rosenfeld_Groebner] we find out that there is a singular solution.

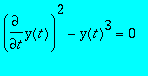
> p := diff(y(t),t)^2 - y(t)^3:

> equations(Rosenfeld_Groebner([p],R));

Plotting the solutions, we realize that the singular solution is not an envelope of the non-singular solution.

> plot({seq(4/(t-3*_C1)^2, _C1=-3..3)},t=-15..15, 0..1/2);

As before, we determine a minimal description of the solution set.

> equations(essential_components(p,R));

It appears that the singular solution does not belong to this minimal description. And indeed, the graph of the non-singular solutions along the zero function is very much alike in the previous example: the non-singular solutions collapse on the zero function. In both cases, the singular solution is a limit of the non-singular solution. It is in that sense that the singular solution here is embedded in the general solution.

Clairaut partial differential equation

Similar enveloping and limitting properties can be found for singular solutions of partial differential equations.

Consider first a pde of Clairaut type:

> pde := -y(t,s)+t*diff(y(t,s),t)+s*diff(y(t,s),s)-diff(y(t,s),t)^2 -diff(y(t,s),s)^2;

> Q := differential_ring(ranking=[y],derivations=[s,t],notation=diff):

> equations(Rosenfeld_Groebner( [pde], Q));

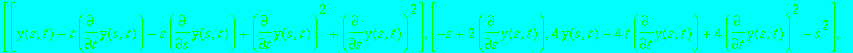
The solutions are:

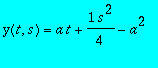
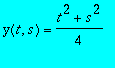
See in the animation below the enveloping property of the singular solution. The moving plane is a non-singular surface integral.

> equations(essential_components(pde,Q));

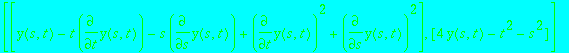
> plots[animate3d]({(t^2+s^2)/4, a/2*t-(a/4)^2*s-(a/2)^2-(a/4)^4},t=-4..4,s=-4..4, a=-5..3,orientation=[45,111]):

Particular solution of a pde

We now illustrate the possible limiting property of a singular solution to a partial differential equation.

> pde := diff(y(s,t),s)^2-diff(y(s,t),t)^2+ y(t,s)^3;

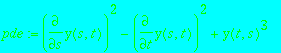
The general solution can be given as:

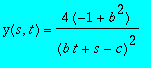
There is furthermore a singular solution:

> Q := differential_ring(ranking=[y],derivations=[s,t],notation=diff):

> equations(Rosenfeld_Groebner([pde],Q));

Nonetheless, the singular solution does not belong to the minimal description of the solution set.

> equations(essential_components(pde,Q));

Indeed, the singular solution is embedded in the general solution, as shown in the following animation where non-singular solutions collapse smoothly on the singular solution.

> plots[animate3d]({0, -4*(-1+(1+1/(c/2))^2)/((1+1/(c/2))*t+s-c/2)},s=-1..0,t=-1..0,c=1..10,orientation=[45,69]):

Higher order differential equations

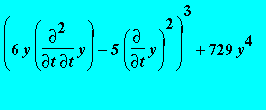
> ode := (6*y(t)*diff(y(t),t,t)-5*diff(y(t),t)^2)^3+729*y(t)^4;

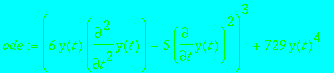
> equations(Rosenfeld_Groebner([ode],R));

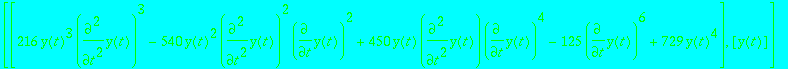
> plot( {seq(seq(((x-a)+b/2*(x-a)^2)^3, a=-1..1), b=2..4)}, x=-2..12/10, -2/100..2/100);

>

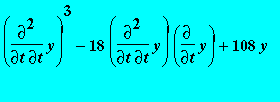
> ode := diff(y(t),t,t)^3-18*diff(y(t),t,t)*diff(y(t),t)+108*y(t);

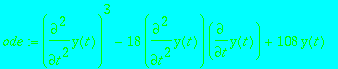
> equations(Rosenfeld_Groebner([ode],R));

>

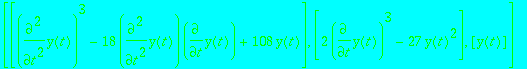
Non-singular solutions and first order singular solution

> ps1b:=plot({x^3/2},x=-7/10..7/10,-1/10..1/10, thickness=2): enps1:=plot({(x)^3,(x+1/3)^3+1/3*(x+1/3),(x+1/3)^3-1/24*(x+1/3),(x-1/3)^3+1/3*(x-1/3),(x-1/3)^3-1/24*(x-1/3)},x=-7/10..7/10,-1/10..1/10):plots[display]({ps1b,enps1}, tickmarks=[4,4]);

Non-singular solutions and zero order singular solution

> plot({seq( (x-1/2)^3+c/3*(x-1/2),c=-1..1), seq((x+1/2)^3+c/3*(x+1/2),c=-1..1)},x=-1..1,-1/4..1/4);

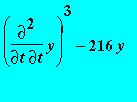
> ode := diff(y(t),t,t)^3-216*y(t);

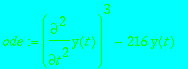
> equations(Rosenfeld_Groebner([ode],R));

> plot( {seq((x+a)^3,a=-1..1), seq(-(x+a)^3,a=-1..1)}, x=-2..2, -1..1);

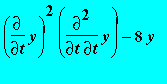
> ode := diff(y(t),t)^2*diff(y(t),t,t)-8*y(t);

> equations(Rosenfeld_Groebner([ode],R));

> plot( {seq((x+a)^2,a=-1..1), seq(-(x+a)^2,a=-1..1)}, x=-2..2, -1..1);

>

Preparation polynomial

Some sophisticated results of differential algebra allow us to say that the properties of singular solution can be determined in the way the equation of the singular solution appear algebraically in the differential equation under consideration. This algebraic structure is revealed by the p reparation polynomial that can be computed by a command of the diffalg package.

We illustrate here the fact that the preparation polynomial is not unique.

> R1 := differential_ring(ranking=[y, z], derivations=[s,t]):

> R2 := differential_ring(ranking=[y, z], derivations=[t,s]):

> p := y[s,t]*y[s,s]+y[t,t]^2;

> a := y[s]+y[t];

> preparation_polynomial(p,z[]=a, R1);

> preparation_polynomial(p,z[]=a, R2);

Computing a minimal decomposition

From a decomposition of the solution set by diffalg[Roenfeld_Groebner] we can determine a minimal decomposition with the following ingredients: the computation of preparation polynomials, application of the regular component theorem (E.Hubert 99), the low power theorem for regular differential polynomials (Hubert 99).

We illustrate the process in two examples.

An ordinary differential equation (back to tobogganing)

> with(diffalg);

> R := differential_ring(ranking=[y,z],derivations=[t]):

> p := y[t]^2+2/3*y[]^3-2*y[]^2+3/2*y[]-1/3;

> G := equations(Rosenfeld_Groebner([p],R));

> a := 2*y[]^2-5*y[]+2;

> pp := preparation_polynomial(p, z[]=a,R);

> hat_a := gcd( coeff(pp, z[]), a); tilde_a := normal(a / hat_a);

By LPT is an essential regular component.

What about ?

> pp := preparation_polynomial(p, z[]=hat_a,R);

By LPT (Hubert 97) is redundant.

The essentiality or redundancy properties of the singular solutions reflect in the behaviour of the non-singular solutions around the singular solution.

is an envelope of the non-singular solutions.

is a limit of non-singular solutions.

> plot({2,1/2,seq(2-3/2*tanh(1/2*(y-C))^2,C=-4..3), seq(2-3/2*coth(1/2*(y-C))^2,C=-4..3) },y=-4..4, -3/2..5/2);

A partial differential polynomial

In this example we will see that, just as the Rosenfeld_Groebner decomposition depends on the ranking, so does the minimal characteristic decomposition. Nonetheless, the underlying prime decomposition of the minimal characteristic decompositions is unique.

> restart;with(diffalg):

> pp := expand(-y[s]*y[t]+y[s]^2+y[]*y[s,s]*y[s]*y[t]-2*y[s]*y[t]*y[]*y[s,t]+ y[s]*y[t]*y[]*y[t,t]+4*y[s]^2*y[s,s]*y[s,t]-2*y[s]^2*y[s,s]*y[t,t]-2*y[s]^2*y[s,s]*y[t]+3*y[s]*y[s,s]*y[t]^2+y[s,s]*y[t]^2*y[s,t]+y[s]*y[s,t]^2*y[t]+y[s]^2*y[s,t]*y[t,t]+4*y[s]^2*y[s,t]*y[t]+3*y[s]*y[s,t]^2*y[]-2*y[s]*y[s,t]*y[t]^2+y[s]^2*y[]*y[s,t]-y[s]^2*y[]*y[t,t]+y[]^2*y[s,s]*y[s,t]-y[]*y[s,s]*y[t]^2-y[]^2*y[s,s]*y[t,t]-y[s]^2*y[t]*y[t,t]-y[]*y[s,t]^2*y[t]+y[]*y[s,t]*y[t]^2+y[]^2*y[s,t]*y[t,t]-4*y[s]*y[s,s]*y[s,t]*y[t]-4*y[s]*y[s,s]*y[]*y[s,t]+3*y[s]*y[s,s]*y[]*y[t,t]+y[s,s]*y[t]*y[s]*y[t,t]+2*y[s,s]*y[t]*y[]*y[s,t]-y[s,s]*y[t]*y[]*y[t,t]-2*y[s]*y[s,t]*y[]*y[t,t]+y[s]^3*y[t]-2*y[s]^2*y[t]^2+y[s]*y[t]^3-y[]^2*y[s,t]^2-y[]*y[s]+y[]*y[t]-y[s,s]*y[t]^3-2*y[s]^2*y[s,t]^2-2*y[s]^3*y[s,t]+y[s]^3*y[t,t]):

> ppp := subs(y[s,t]=y[t,s],pp);

> p := evaln(p): alias(`p`=p);

We choose a first ranking:

> alias( p = pp):

> R1 := differential_ring(ranking=[y,z],derivations=[s,t]):

> G1 := equations(Rosenfeld_Groebner([p],R1));

According to the regular component theorem (Hubert 97), we know that is redundant.

Let us study the other singular solution:

> a := y[s]^2-y[s]*y[t]-y[]*y[s]+y[]*y[t];

> preparation_polynomial(p,z[]=a,R1);

By LPT (Hubert 97) : is an essential component.

And, indeed:

> equations(essential_components(p,R1));

With another ranking:

> q;

> alias(q=ppp):

> R2:= differential_ring(ranking=[y,z],derivations=[t,s]):

> G :=equations(Rosenfeld_Groebner([q],R2));

> M := equations(essential_components(q,R2));

This, in appearance is different from the previously obtained minimal characteristic decomposition. Except that the irreducible factors of the differential polynomials appearing in any minimal regular decomposition are the same.

> factor(a);

Universal equation

This equation was brought out by R. Rubel. The solution of this 4th order, homogeneous differential equation of degree 7 has the property that its solution can approximate piecewisely any smooth function.

> rubel := 3*y[x]^4*y[x$2]*y[x$4]^2-4*y[x]^4*y[x$3]^2*y[x$4]
+ 6*y[x]^3*y[x$2]^2*y[x$3]*y[x$4] + 24*y[x]^2*y[x$2]^4*y[x$4]
-12*y[x]^3*y[x$2]*y[x$3]^3-29*y[x]^2*y[x$2]^3*y[x$3]^2+12*y[x$2]^7;

> R := differential_ring(ranking=[y,z], derivations=[x]):

> equations(Rosenfeld_Groebner([rubel], R));

> equations(essential_components(rubel,R));

Only one essential singular solution.

Thus far we can deduce the graphs of the solutions of (the essential singular solution) are envelopes of the non-singular solutions.

Furthermore, we know that the solutions of the redundant singular solution are the limit case of either the essential singular solution or the non-singular solution.

We can extract additional information from the preparation polynomial:

> preparation_polynomial(3*y[x,x]^4+y[x]^2*y[x,x,x]^2, z[]=y[x,x],R);

> preparation_polynomial(rubel, z[]=y[x,x],R);

The straight lines, solutions of are limits of both the non-singular solutions and the essential singular solutions (the leading coefficient theorem).

Chazy equation

This equation arose in Chazy's work to extend the Painleve analysis to 3rd order differential equations.

In doing so he uncovered certain differential equations whose non-singular solution have no movable singularity whereas one of the singular solution has. Here is an example (see Ince).

> chazy := -(y[x,x]+y[]^3*y[x])^2 + (y[]*y[x])^2*(4*y[x]+y[]^4) ;

> R := differential_ring(ranking=[y], derivations=[x]):

> equations(Rosenfeld_Groebner([chazy],R));

> equations(essential_components(chazy,R));

The component appears as redundant, as well as a prime factor of the other singular regular component .

Here, our conclusions are:

- the solutions of are envelopes of the non-singular solutions

- the solution of are limits of non-singular solutions.

- is a limit of both the non-singular solution of the equation and the non-singular solutions of , the essential singular component.

> ode2 := jet2diff(chazy, x);
ode1 := 4*diff(y(x),x)^2+diff(y(x),x)*y(x)^4;
singsol := RootOf(3*_Z^3*(x-C)-4);
odetest(y(x)=singsol, ode1);

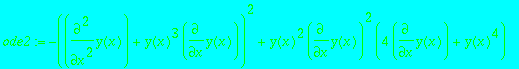
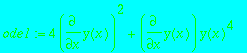
> plot( {seq(C/3, C=-2..2), seq( (4/(3*(x-2*C)))^1/3, C=-2..1)}, x=-3..3, -1..1, title="singular solutions",discont=true);

The hyperbolas are envelopes of the non-singular solutions. The horizontal lines are limits of the nonsingular solutions.

You can check with the closed form solution:

> general_sol := 'A'*tan('A'^3*x+'B');
odetest(y(x)=general_sol, ode2);

>

Travelling wave of the Korteg de Vries equation - Weierstrass elliptic function.

We look for the equation of a solitary wave solution of the KdV equation: .

Let where

We proceed to show first how to obtain the equation for y(s), namely

where and are arbitrary constants.

When , that is when has only simple roots, the non-singular solutions are translation of the Weirstrass elliptic function (WeierstrassP). We study the singular solutions in this generic case and in the degenerate cases, namely and and see how their analyic properties vary.

KdV -> Weierstrass Elliptic

> restart;

> kdv := diff(u(t,x),t)-6*u(t,x)*diff(u(t,x),x)+diff(u(t,x),`$`(x,3));

> wave := 1/2*expand(convert(eval(eval(kdv, u(t,x)= 2*y(x-c*t)-c/6), x=c*t+s),diff));

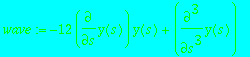
This equation can be integrated into

which in turn has as an integrating factor. Finally, satisfies . We verify this result.

> Wp := diff(y(s),s)^2-4*y(s)^3+g[2]*y(s) +g[3];

> ode2 :=simplify(diff(Wp,s)/(2*(diff(y(s),s))));

> wave - diff(%,s);

Generic case :

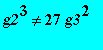
> Wp := diff(w(z),z)^2-4*w(z)^3+g2*w(z) +g3;

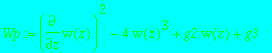
> with(diffalg):
K := field_extension(transcendental_elements=[g2,g3]):
R := differential_ring(ranking=[w],derivations=[z],notation=diff,field_of_constants=K):
equations(Rosenfeld_Groebner([Wp],R));

> equations(essential_components(Wp,R));

• There are three singular zeros: w(z)=ri , where ri is one of the root of of 4*r^3-g2*r-g3 . There are all three essential singular zeros. As such they are envelopes of the non-singular zeros of Wp . This can be observed by plotting the real zeros for g2=4,g3=-1 :

> singsol := {plot({fsolve(-4*r^3+4*r-1,r)},z=-3..3, color=red, thickness=2)}:
galsol1 :={seq(plots[odeplot](dsolve({diff(w(z),z,z)-6*w(z)^2+2,w(ic)=-1,D(w)(ic)=-1.0},
w(z),type=numeric),-3..3,color=blue),ic=0..4)}:
galsol2 := {seq(plots[odeplot](dsolve({diff(w(z),z,z)-6*w(z)^2+2,w(ic)=2,D(w)(ic)=-5.0},
w(z),type=numeric),ic-0.15..ic+1.7,color=green),ic=-3..1)}:
plots[display](singsol union galsol1 union galsol2,title="g2=4,g3=-1",view=[-3..3,-3/2..3]);

>

• We parameterise the equation with g :

> Wps := subs(g2=3*g^2,g3=g^3,Wp);

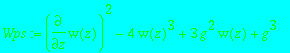
> Ks := field_extension(transcendental_elements=[g]):
Rs := differential_ring(ranking=[w],derivations=[z],notation=diff,field_of_constants=Ks):
equations(Rosenfeld_Groebner([Wps],Rs));

> equations(essential_components(Wps,Rs));

• There are two singular zeros: w(z)=g and w(z)=-g/2 . w(z)=g is an essential singular zero of Wps and therefore is an envelope of the non singular zeros of Wps . On the contrary, the singular zero w(z) =-g/2 of Wps is not essential and therefore is a limiting case of the non singular zeros of Wps .
• We can observe the situation for g=-1 :

> singsol:=plot({-1,1/2},color=red,thickness=2):
galsol1:=plot({seq(-1+3/2*tanh(1/2*(C-z)*sqrt(6))^2,C=-1..1)},z=-3..3,color=green):
galsol2:=plot({seq(-1+3/2*coth(1/2*(C-z)*sqrt(6))^2,C=-1..1)},z=-3..3,color=blue):
plots[display]({singsol,galsol1,galsol2},view=[-3..3,-3/2..3],title="g2=3,g3=-1");

>

• The equation is now:

> Wp0:=subs(g2=0,g3=0,Wp);

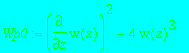
> R0 := differential_ring(ranking=[w],derivations=[z],notation=diff):
equations(Rosenfeld_Groebner([Wp0],R0));

> equations(essential_components(Wp0,R0));

• There is only one singular zero, w(z)=0 , and it is not essential. We can see its limiting property with respect to the non singular zeros.

> singsol:=plot(0,s=-4..4, color=red, thickness=2):
galsol:= plot({seq(1/((z-C)^2),C=-2..1)},z=-4..4):
plots[display]({singsol,galsol},view=[-4..4,-1/2..2]);