Computing singular solutions

Consider the following Clairaut partial differential equation:

>	u(x,y) = x*diff(u(x,y),x)+y*diff(u(x,y),y)+diff(u(x,y),x)*diff(u(x,y),y) ;

We represent it by the differential polynomial p with a more compact syntax, called jet notation.

>	p := -u[]+x*u[x]+y*u[y]+u[x]*u[y];

Before any manipulation of this differential polynomial we define a differential polynomial ring it belongs to:

>	R := differential_ring(ranking=[u], derivations=[x,y], notation=jet);

The Clairaut equation under consideration has a singular solution. This will be unveiled by Rosenfeld_Groebner. The result of Rosenfeld_Groebner is a list of tables (appearing as characterisable), each defining a characterisable component.

>	Clairaut := Rosenfeld_Groebner({p}, R);

Each characterisable component is defined by a differential characteristic set that can be accessed via the equations command. The non singular zeros of this differential characteristic set are the zeros that do not make vanish some additional differential polynomials that can be accessed via the inequations command.

>	equations(Clairaut[1]), inequations(Clairaut[1]);

>	equations(Clairaut[2]), inequations(Clairaut[2]);

The second component represents the singular solution of this Clairaut equation while the first represents the general solution of the Clairaut equation.

Detection of inconsistencies in a differential system

Consider the 3 following differential polynomials:

>	p1:=diff(u(x,y),x)+v(x,y)-y;

>	p2:=diff(u(x,y),y)+v(x,y);

>	p3:=diff(v(x,y),x)-diff(v(x,y),y);

They define the system of differential equations S : p1 = 0, p2 = 0, p3 = 0.

Before any manipulation of these differential polynomials we define a structure they belong to. We have the possibility to work with the Maple notation of derivatives.

>	R := differential_ring(ranking=[u,v], derivations=[x,y], notation=diff);

Note that we can convert to the jet notation, introduced in the previous example:

>	denote(p1, 'jet', R), denote(p2, 'jet', R), denote(p3, 'jet', R);

What does Rosenfeld_Groebner tell us about the system S?

>	Rosenfeld_Groebner({p1,p2,p3}, R);

This indicates that the system bears a contradiction: p1, p2, p3 have no common zero.

In this case it is quite easy to detect the contradiction.

Differentiating p1 according to y we obtain:

>	differentiate(p1, y, R);

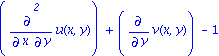
The meromorphic solutions of S, if they exist, shall make this differential polynomial vanish. They shall also make the following differential polynomial vanish

>	differentiate(p2, x, R)- p3;

The two equations can not be satisfied simultaneously: the system S bears here a contradiction 1=0 and therefore admits no solution.

Solving ordinary differential systems: Elimination ranking

To perform a chain resolution of a system of ordinary differential equations one shall use an elimination ranking.

Consider the differential system defined by the following set S of differential polynomials in the unknown functions x(t),y(t),z(t).

>	S := [diff(x(t),t)-x(t)*(x(t)+y(t)),diff(y(t),t)+y(t)*(x(t)+y(t)), diff(x(t),t)^2+ diff(y(t),t)^2+ diff(z(t),t)^2-1 ];

Using an elimination ranking where z(t)>y(t)>x(t) we will obtain differential characteristic sets containing a differential polynomial in x(t) alone, a differential polynomial determining y(t) in terms of x(t) and finally a differential polynomial determining z(t) in terms of y(t) and x(t)

To see more clearly the dependencies of these differential polynomials, one can use the rewrite_rules command, which is an alternative to the equations command.

>	R := differential_ring(ranking=[z,y,x], derivations=[t], notation=diff): G :=Rosenfeld_Groebner(S, R);

>	rewrite_rules(G[1]); inequations(G[1]);

>	rewrite_rules(G[2]); inequations(G[2]);

We can perform a chain resolution to both components of the result. Note that the singular solution x(t)=0 has to be discarded in the resolution of the first component, as indicated by the differential polynomials of its inequations. The correct complete solution with x(t)=0 is given by the second component.

Constrained systems: Orderly and mixed rankings

Consider the set of differential polynomials describing the motion of a pendulum, i.e. a point mass m suspended at a massless rod of length l under the influence of gravity g, in Cartesian coordinates (x,y). The Lagrangian formulation leads to two second order differential equations together with an algebraic constraint. T is the Lagrangian multiplier.

>	P := [m*diff(y(t),t,t)+T(t)*y(t)+g, m*diff(x(t),t,t)+T(t)*x(t), x(t)^2+y(t)^2-l^2];

To be in a position to manipulate this system we have to declare the additional constants m, l, g appearing in the coefficients of these differential polynomials.

>	K := field_extension(transcendental_elements=[m,l,g]);

Orderly ranking

If one wishes to find the lowest order differential polynomials vanishing on the zeros of the system modelling the pendulum and in particular all the algebraic constraints (i.e. the differential polynomials of order 0) one shall use an orderly ranking.

>	RO := differential_ring(ranking=[[T,x,y]], derivations=[t], field_of_constants=K, notation=diff): GO:= Rosenfeld_Groebner(P, RO);

>	rewrite_rules(GO[1]); inequations(GO[1]);

>	rewrite_rules(GO[2]); inequations(GO[2]);

The second component in the output of Rosenfeld_Groebner corresponds to the equilibria of the pendulum. From the first component of the output we see that the actual motion is described by two first order differential equations together with a constraint: the solution depends on only two arbitrary constants.

Mixed ranking

If we wish to obtain the differential system satisfied by x and y alone one shall eliminate T:

>	RM := differential_ring(ranking=[T,[x,y]], derivations=[t], field_of_constants=K, notation=diff): GM:= Rosenfeld_Groebner(P, RM);

>	rewrite_rules(GM[1]);

>	rewrite_rules(GM[2]);

Note here that the motion is given by a second order differential equation in y(t). Then the Lagrange multiplier is given explicitely in terms of y(t) and its first derivative.

Solving partial differential system: Lexicographic ranking

To solve overdetermined systems of partial differential equations it is interesting to compute first the ordinary differential equations satisfied by the solutions of the system. A lexicographic ranking has to be chosen to this end.

Consider the differential system S defining the infinitesimal generators of the symmetry group of the Burgers equations:

>	Burgers_pde := Diff(u(t,x),t)=Diff(u(t,x),x,x)-u(t,x)*Diff(u(t,x),x);

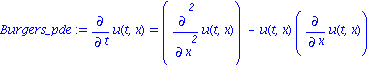
>	with(liesymm): BurgersSymm := determine(Burgers_pde, `V`, u(t,x), [ux, ut]);

Warning, the protected name close has been redefined and
unprotected

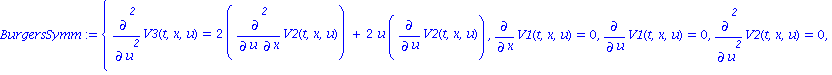
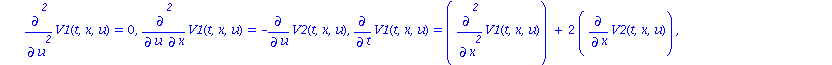
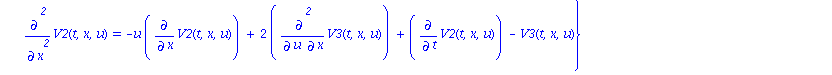
Let us seek the ordinary differential equations with respect to t satisfied by the solutions of this system.

>	R := differential_ring(ranking=[lex[V3,V2,V1]], derivations=[u,x,t], notation=Diff);

>	G := Rosenfeld_Groebner(map(eq->rhs(eq)-lhs(eq),BurgersSymm),R);

>	rewrite_rules(G[1]);

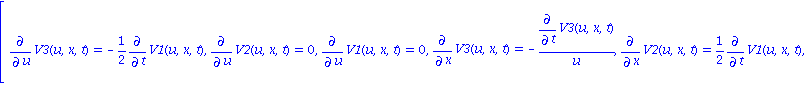
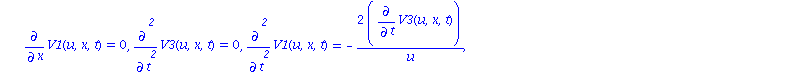
We can see that there are three independent ordinary differential polynomials with respect to t (the last three of the differential characteristic set). All other ordinary (in t) differential polynomials vanishing on the solutions of BurgersSymm can be written as linear combination of these three ones together with their derivatives.