Linear Representation & SAB 

>

 

 

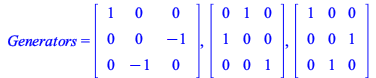	(1.4.1.1)

 

Lists with symmetry adapted basis grouped by degree for the polynomial and polynomials maps*(See Symmetry in Multivariate Ideal Interpolation Section 5.3).
These bases are passed as parameters to the SymmetryAdaptedHBasis method; 

>

tim := time(): SymmetryAdaptedPolynomialList := [seq(SAPolynomialBasis(Rep, Irr, i .. i)[1], i=0..7)]:    time() - tim; `Multiplicities within a degree` = [seq(map(p -> nops(p[1]), SymmetryAdaptedPolynomialList[i + 1]), i=0..7)];     tim := time(): SymmetryAdaptedPolynomialMapList := SAPolynomialMapCollection(Rep, Irr, 0..4):     time() - tim;

 

 

 

	(1.4.1.2)

 

The latter computation is  time consuming.Yet if we deal with a reflection group this  is not needed as the H-basis will contain  then only invariants.  

We then need  only SymmetryAdaptedPolynomialList, in the appropriate format. This is obtained  as: 

>	SymmetryAdaptedPolynomialMapList :=  fromSABPolyToSABMap(SymmetryAdaptedPolynomialList):

 

Linear Forms 

>

 

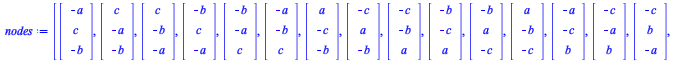(1.4.2.1)

 

Invariants and Equivariants by Interpolation 

>

 

>	map(primpart,Flatten(H));

 

(1.4.3.1)

 

>

 

(1.4.3.2)

 

>

 

(1.4.3.3)