Example 6.4: D6 acting on R^3
Linear Action & SAB
| > |
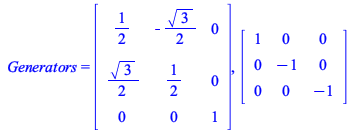 |
|
| (3.1.1.1) |
| > |
| (3.1.1.2) |
Invariants and Equivariants
| > |
| > |
| (3.1.2.1) |
| > |
| (3.1.2.2) |
Example 6.4: D6 acting on R^3
Linear Action & SAB
| > |
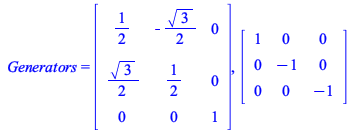 |
|
| (3.1.1.1) |
| > |
| (3.1.1.2) |
Invariants and Equivariants
| > |
| > |
| (3.1.2.1) |
| > |
| (3.1.2.2) |