Array

Tipi

String s;
int [] ints;
String [] strs;

Creazione

int [] ints = new int[42];
int [] strs = new String[10];

Inizializzazione

int [] ints = new int[10];

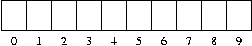
ints[0] = 4;
ints[5]=6;

Valore di default

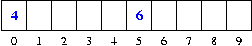
per int è 0

per char è \0

per oggetto è null

Valore immediato

int [] primes = {2, 3, 5, 7};

int [] primes = new int[4];
primes[0]=2;
primes[1]=3;
primes[2]=5;
primes[3]=7;

String [] strs = {"Hello", null, "World"};

String [] strs = new String[3];
strs[0]="Hello";
strs[2]="World";

Assegnazione

int [] is;
is = new int[]{2, 4};

int [] is = {2, 4};

Lunghezza

void filledArray (int[] ar) {
  for (int i=0; i < ar.length; i++)
    ar[i]=i;
}

Array multidimensionale

int [] [] ints;
String [] [] s = { {"a", "b", "c"}, {"d", "e", "f"}};
String [] [] s = new String[2][2];

int [] [] expandList (Point [] pts) {
  int [] [] res = new int [pts.length][2];
  for (int i=0; i < pts.length; i++) {
    res[i][0]=pts[i].x;
    res[i][1]=pts[i].y;
  }
  return res;
}

int [] [] createArray (int n) {
  int [] [] res = new int [n] [];
  for (int i=0; i < n; i++) {
    res[i] = new int [i+1];
  }
}

Esercizi

B2. Scrivere un metodo checkSequence che prende un array di numeri interi e un numero intero n e ritorna vero se n valori consecutivi dell'array sono gli stessi.
Ex: con {2, 3, 3, 5} e 2, checkSequence ritorna true ma con {2, 3, 3, 4} e 3 ritorna false.

B3. Scrivere un metodo equals che prende due array di numeri interi e ritorna vero se i due array hanno gli stessi valori nelle stesse posizioni.
Ex: con {2, 3, 3} e {2, 3, 3}, equals ritorna true ma con {2, 3, 3} e {2} ritorna false.

B4. Scrivere un metodo equals2 che prende due array bidimensionali di numeri interi (int [][]) e ritorna vero se i due array hanno gli stessi valori nelle stesse posizioni.
Ex: con {{2, 3}, {3}} e {{2, 3}, {3}}, equals2 ritorna true ma con {{2, 3}, {3}} e {{2}} ritorna false.

B5. Scrivere un metodo firstPrime che prende un numero intero n e ritorna un array contenente i primi n numeri primi.
Ex: con 3, firstPrime ritorna {2, 3, 5} ma con 5 ritorna {2, 3, 5, 7, 11}. Se può usare il metodo isPrime definito nell'esercizio A1.

B6. Scrivere un metodo lessPrime che prende un numero intero n e ritorna un array contenente i primi numeri primi minori di n.
Ex: con 3, lessPrime ritorna {2} ma con 20 ritorna {2, 3, 5, 7, 11, 13, 17, 19}. Se può usare il metodo isPrime definito nell'esercizio A1.

B7*. Scrivere un metodo checkSym che prende un array bidimensionale non necessariamente quadrato di numeri interi e restituisce un booleano. Tale booleano vale true quando c'è una simmetria fra righe e colonne: la riga i e la colonna i hanno esattamente gli stessi numeri nello stesso ordine per ogni i.
Per esempio, dato l'array {{1, 2, 3}, {2, 1}, {3}}, il metodo restituisce true mentre, dato l'array {{1, 2, 3}}, il metodo restituisce false.

B8*. Scrivere un metodo magicSquare che prende un array bidimensionale quadrato di numeri interi e restituisce un booleano. Tale booleano vale true quando l'array rappresenta un quadrato magico: la somma dei numeri di una qualunque riga, colonna o diagonale dà lo stesso risultato. Per esempio, dato l'array {{8, 1, 6}, {3, 5, 7}, {4, 9, 2}}, il metodo restituisce true.

B9*. Scrivere un metodo triangle che prende un array bidimensionale di numeri interi e restituisce un booleano. Tale booleano vale true quando l'array rappresenta un triangolo, ovvero la lunghezza della prima riga è uno, la lunghezza della seconda riga è due, etc. Per esempio, dato l'array {{8}, {3, 5}, {4, 9, 2}}, il metodo restituisce true.

B10*. Scrivere un metodo isBordered che prende un array bidimensionale quadrato di numeri interi e restituisce un booleano. Tale booleano vale true quando l'array è composto di bordi successivi di interi dello stesso valore, false altrimenti. Per esempio, dato l'array
{{4,  4,  4,  4,  4, 4},
 {4, -2, -2, -2, -2, 4},
 {4, -2,  0,  0, -2, 4},
 {4, -2, -2, -2, -2, 4},
 {4,  4,  4,  4,  4, 4}}
il metodo restituisce true.

B11*. Scrivere un metodo statico divide che, dati due array unidimensionali di numeri interi, restituisce true se per ogni elemento b del secondo array esiste esattamente un elemento a del primo array tale che a divide b. Altrimenti il metodo restituisce false. Per esempio, {2, 3} divide {2, 3, 4, 8, 9} ma non divide {2, 3, 4, 6, 8, 9}.