



Next: The NonLinear procedure
Up: Solving systems with linear
Previous: Mathematical background
Contents
The procedure is implemented as:
int Solve_Simplex(int m,int n,int NbNl,
INTEGER_VECTOR TypeEq,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
void (* NonLinear)(INTERVAL_VECTOR &x,INTERVAL_VECTOR &X),
void (* CoeffLinear)(MATRIX &U),
double MaxDiam,
int FullSimplex,
INTERVAL_VECTOR & TheDomain,
int Order,int Iteration,int Stop,
double epsilon,double epsilonf,double Dist,
INTERVAL_MATRIX & Solution,int Nb,
int (* Simp_Proc)(INTERVAL_VECTOR &))
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- NbNl: number of equations that have no linear term at
all or are inequalities.
If you omit this parameter its value will be assumed to be 0 and
you have to omit the TypeEq parameter.
- TypeEq: an array of integers that indicate the type for
the equations. TypeEq(i) is -1,0,1 if equation i is an
inequality
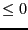 , an equation or an inequality
, an equation or an inequality 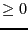 .
.
- IntervalFunction: a function which return the interval
vector evaluation of the equations, see the note 2.3.4.3 on how
to write this procedure. The equations must be ordered: first
the equations with linear terms then the equations
without any linear terms and finally the inequalities
- NonLinear: a procedure to compute the non linear part of
the equations, see note 2.14.2.1
- CoeffLinear: a procedure that return a matrix which
contain the constant coefficients of the linear term in the equation,
see note 2.14.2.2
- MaxDiam: the simplex method will not be used on boxes
whose maximal width is lower than this value. Should be set
to 0 or a small value
- FullSimplex: this flag is used to indicate how much we
will
use the simplex method (which may be costly). If set to -1 only the
phase I of the simplex will be used. If set to
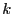 with
with 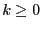 , then
the full simplex method will be used recursively on the
, then
the full simplex method will be used recursively on the 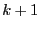 variables having the largest interval width.
variables having the largest interval width.
- TheDomain: box in which we are looking for
solution of the equations
- Order: the type of order which is used to store the
intervals created during the bisection process. This order may be
either MAX_FUNCTION_ORDER or MAX_MIDDLE_FUNCTION_ORDER. See the note on the order 2.3.4.4.
- M: the maximum number of boxes which may be
stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has
been found
- 2: the algorithm will stop as soon as Nb solutions
have been found
- epsilon: the maximal width of the solution intervals, see the
note 2.3.4.6
- epsilonf: the maximal width of the equation intervals for
a solution, see the
note 2.3.4.6
- Dist: minimal distance between the middle point of two
interval solutions, see the note 2.3.4.7
- Solution: an interval matrix of size (Nb,m)
which will contained the solution intervals. This list is sorted using
the order specified by Order
- Nb: the maximal number of solution which will be returned
by the algorithm
- Simp_Proc: a user-supplied procedure that take as input
the current box and proceed to some further reduction of
the width of the box or even determine that there is no
solution for this box, in which case it should return
-1 (see note 2.3.3).
Remember that you may use the 3B method to improve the efficiency of
this algorithm (see section 2.3.2).
Note that the Simp_Proc argument may be omitted.
Subsections




Next: The NonLinear procedure
Up: Solving systems with linear
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20