



Next: Examples
Up: Solving trigonometric equation
Previous: Mathematical background
Contents
The purpose of this procedure is to determine the roots of a
trigonometric equation within a given angle interval.
int Solve_Trigo_Interval(int n,VECTOR &A,INTEGER_VECTOR &SSin,
INTEGER_VECTOR &CCos,double epsilon,double epsilonf,
int M,int Stop,INTERVAL_VECTOR &Solution,int Nb,REAL Inf,REAL Sup);
with:
- M: the maximum number of boxes which may be
stored. See the note 2.3.4.5
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in the
angle interval
- 1: the algorithm will stop as soon as 1 solution has
been found
- 2: the algorithm will stop as soon as Nb solutions
have been found
- epsilon: the maximal width of the box, see the
note 2.3.4.6
- epsilonf: the maximal width of the equation intervals, see the
note 2.3.4.6
- Solution: an interval vector of size at least Nb
which will contained the solution intervals.
- Nb: the maximal number of solution which will be returned
by the algorithm
- Inf, Sup: the bound of the angle interval in which we are
looking for solutions.
Note that the returned Solution will always be a range
[a,b] included in [0,2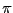 ] and in [Inf,Sup], this
interval angle being reduced to an angle interval in the range [0,2
] and in [Inf,Sup], this
interval angle being reduced to an angle interval in the range [0,2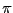 ].
The procedure will return:
].
The procedure will return:
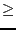 0: the number of roots
0: the number of roots
- -1: the bound Inf or Sup is incorrect (positive or
negative infinity)
If you are looking for all the roots of the trigonometric equation you
may either specify [Inf,Sup] as [0,2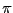 ] or use the procedure:
] or use the procedure:
int Solve_Trigo_Interval(int n,VECTOR &A,INTEGER_VECTOR &SSin,
INTEGER_VECTOR &CCos,double epsilon,double epsilonf,
int M,int Stop,INTERVAL_VECTOR &Solution,int Nb);
This procedure first analyze the trigonometric equation to find bounds
on the roots using the algorithm described in
section 4.3, then use the previous procedure to
determine the roots within the bound. In some case this procedure may
be faster than the general purpose algorithm.




Next: Examples
Up: Solving trigonometric equation
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20