Problems with the interval-valuation of an expression

Next: Dealing with infinity Up: Interval Analysis Previous: Implementation

La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de COPRIN

COPRIN home page

La page "Présentation" de l'INRIA

INRIA home page

Problems with the interval-valuation of an expression

An important point is that not all expressions can be evaluated using interval arithmetics. Namely constraints that prohibits the interval evaluation of an expression are:

denominator that may include 0
argument of square should be positive
argument of arcsin and arccos should be included in [-1,1]
argument of log,ln,log10 should be positive
argument of arccosh should be greater than 1
argument of arctanh cannot include the interval [-1,1]
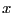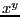argument of where 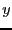is not an integer should be
argument 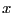of 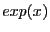should not be too large to avoid overflow problem.

If such situation occurs a fatal error will be generated at run time. Hence such special cases has to be dealt with carefully. ALIAS-Maple offers the possibility of dealing with such problem. For example the procedure Problem_Expression allows one to determine what constraints should be satisfied by the unknowns so that each equations can be interval evaluated, see the ALIAS-Maple documentation.

If you use your own evaluation procedure and are aware of evaluation problems and modify the returned values if such case occurs it will be a good policy to set C++ flags ALIAS_ChangeF, ALIAS_ChangeJ to 1 (default value 0) if a change occurs. Currently the interval Newton scheme that is embedded in some of the solving procedures of ALIAS will not be used if one of these flags is set to 1 during the calculation.