



Next: Implementation
Up: Ridder method for solving
Previous: Ridder method for solving
Contents
Ridder method is an iterative scheme used to obtain one root of the
equation 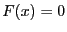 within an interval
within an interval ![$[x_1,x_2]$](img278.png) . It assumes that
. It assumes that
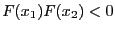 . Let
. Let 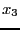 be the mid-point of the interval
be the mid-point of the interval
![$[x_1,x_2]$](img278.png) . A new estimate of the root is
. A new estimate of the root is 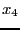 with:
with:
under the assumption
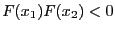 it may be seen that
it may be seen that 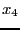 is
guaranteed to lie within the interval
is
guaranteed to lie within the interval ![$[x_1,x_2]$](img278.png) . As soon as
. As soon as 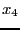 as
been determined we choose as new
as
been determined we choose as new ![$[x_1,x_2]$](img278.png) the interval
the interval ![$[x_1,x_4]$](img283.png) if
if
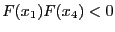 or
or ![$[x_4,x_2]$](img285.png) if
if
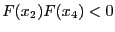 . The convergence
of this algorithm is quadratic.
. The convergence
of this algorithm is quadratic.
Jean-Pierre Merlet
2012-12-20