



Next: Jacobian matrix
Up: Implementation
Previous: Implementation
Contents
The procedure will return an integer 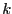
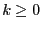 : number of solutions
: number of solutions
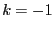 : the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
: the size of the storage is too low (
possible solutions: increase M,
or use the 3B method, or use the reverse storage mode or the single
bisection mode)
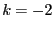 : m or n is not strictly positive
: m or n is not strictly positive
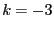 : Order is not 0 or 1
: Order is not 0 or 1
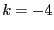 : one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, an inequality
: one of the function in the system has not a type 0, -1
or 1 (i.e. it's not an equation, an inequality 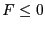 or an
inequality
or an
inequality 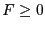 )
)
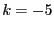 : we are in the optimization mode and more than one
functions are expressions to be optimized (see the Optimization chapter)
: we are in the optimization mode and more than one
functions are expressions to be optimized (see the Optimization chapter)
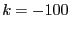 : in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
: in the mixed bisection mode the number of variables
that will be bisected is larger than the number of unknowns
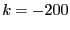 : one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
: one of the value of ALIAS_Delta3B or
ALIAS_Max3B is negative or 0
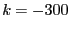 : one of the value of ALIAS_SubEq3B is not 0 or 1
: one of the value of ALIAS_SubEq3B is not 0 or 1
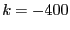 : although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
: although ALIAS_SubEq3B has as size the number of
equations none of its components is 1
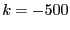 : ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
: ALIAS_ND is different from 0 (i.e. we are
dealing with a non-0 dimensional problem, see the corresponding
chapter) and the name of the result file has not been specified
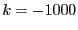 : the value of the flag Single_Bisection is not
correct
: the value of the flag Single_Bisection is not
correct
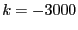 : we use the full bisection mode and the problem has
more than 10 unknowns
: we use the full bisection mode and the problem has
more than 10 unknowns
The following variables play also a role in the computation:
- ALIAS_Store_Gradient: if not 0 the gradient matrix of
each box will be stored together with the input
intervals. Must be set to 0 for large problem
(default value: 1)
- ALIAS_Diam_Max_Gradient: if the maximal width of the
ranges in a box is lower than this value, then the
gradient will be used to perform the interval evaluation of the
functions (default value: 1.e10)
- ALIAS_Diam_Max_Kraw: if the maximal width of the
ranges in a box is lower than this value, then the
Krawczyk operator will be used to determine if there is a unique
solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the
ranges in a box is lower than this value, then the
interval Newton method will be used either to try to reduce
the width of the box or to to ensure that there is no solution of the
system in the box (default value: 1.e10)




Next: Jacobian matrix
Up: Implementation
Previous: Implementation
Contents
Jean-Pierre Merlet
2012-12-20