Example 4

Next: General comments Up: Examples and Troubleshooting Previous: Example 3

La page de J-P. Merlet

J-P. Merlet home page

La page Présentation de COPRIN

COPRIN home page

La page "Présentation" de l'INRIA

INRIA home page

Example 4

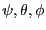In this example (see section 15.1.3) we deal with a complex problem of three equations in three unknowns $\psi,\theta,\phi$ . We are looking for a solution in the domain:

$\begin{displaymath}[4.537856054,4.886921908], [1.570796327,1.745329252], [0.6981317008, 0.8726646262] \end{displaymath}$

The system has a solution which is approximately:

$\begin{displaymath} 4.6616603883, 1.70089818026, 0.86938888189 \end{displaymath}$

This problem is extremely ill conditioned as for the TestDomain the functions intervals are:

$\begin{displaymath}[-1.45096e+08,1.32527e+08]; [-38293.3,29151.5] ; [-36389.1,27705.7] \end{displaymath}$

This program is implemented under the name Test_Solve_General. With espsilonf=0 and epsilon=0.001 and if we stop at the first solution we find with the maximum equation ordering:

$\begin{displaymath} \psi=[4.664665,4.665347]~~~~ \theta=[1.7034,1.703741]~~~~ \phi=[0.8706193,0.8709602] \end{displaymath}$

with 531 boxes. We may also mention the following remarks:

we get no improvement with the single bisection mode as we need 2435 boxes to find the first solution,
using the Reverse Storage mode does not lead to any improvement for finding the first root: in this mode we need 5587 boxes to get the first solution,

With the maximum middle-point equation ordering we find:

$\begin{displaymath} \psi=[4.665347,4.666029]~~~~ \theta=[1.701355,1.701696]~~~~ \phi=[0.8709602,0.8713011]~~~~ \end{displaymath}$

with 203 boxes. The importance of normalizing the functions appears if we use epsilonf=0.1 and epsilon=0. If we stop at the first solution we find:

$\begin{eqnarray*} &&\psi=[4.661660388259656,4.661660388340929]\\ &&\theta=[1.70... ...00898180284073]\\ &&\phi=[0.869388881899751,0.869388881940387] \end{eqnarray*}$

while if we divide the first function by 1000 we find:

$\begin{eqnarray*} &&\psi=[4.661658091884636,4.661658424779772]\\ &&\theta=[1.70... ...00898570395561]\\ &&\phi=[0.869388105618527,0.869388272066095] \end{eqnarray*}$

in four time less computation time.