



Next: Miscellaneous procedures
Up: Definite integrals
Previous: Integral with one variable
Contents
Integral with multiple variable
ALIAS offers 4 procedures to compute definite integral with more
than one variable.
int IntegrateMultiRectangle(
INTERVAL_VECTOR (* Function)
(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR (* Second_Derivative)
(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Iteration,
double Accuracy,
INTERVAL & Result)
int IntegrateMultiRectangle(
INTERVAL_VECTOR (* Function)
(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR (* Second_Derivative)
(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Iteration,
double Accuracy,
INTERVAL & Result)
In the second form Gradient is a procedure in MakeJ format
that allows to compute the derivatives of the second derivatives of
the function.
ALIAS offer also procedure based on Taylor expansion of the
function.
int IntegrateMultiTaylor(
INTERVAL_VECTOR (* CoeffInt)
(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR (* RestTaylor)
(int,int,INTERVAL_VECTOR &),
INTEGER_MATRIX &APOWERINT,
INTEGER_MATRIX &APOWERREM,
int nbrem,
int Order,
INTERVAL_VECTOR & TheDomain,
int Iteration,
double Accuracy,
INTERVAL & Result)
int IntegrateMultiTaylor(
INTERVAL_VECTOR (* CoeffInt)
(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR (* RestTaylor)
(int,int,INTERVAL_VECTOR &),
INTEGER_MATRIX &APOWERINT,
int Order,
INTERVAL_VECTOR & TheDomain,
int Iteration,
double Accuracy,
INTERVAL & Result)
The Taylor expansion of the function 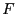 may be written as:
may be written as:
- CoeffInt: a procedure in MakeF format that compute
the coefficients
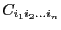
- APOWERINT: a table with the exponent
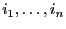 for
each term
for
each term
- RestTaylor, APOWERREM: in the first form they play the same
role than CoeffInt, APOWERINT for the remainder. There is
nbrem terms in the remainder
- RestTaylor: in the second form a procedure in MakeF
format that compute the remainder
- Order: the degree of the remainder
Jean-Pierre Merlet
2012-12-20