



Next: Missed branches
Up: Implementation
Previous: Procedure for following branches
Contents
Full continuation procedure
This procedure will determine initial points on the branches of the
system for the value
of the parameter within some bounds and then follow the branches. It
is implemented as
int ALIAS_Full_Continuation(int m,int n,
INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* IntervalHessian)(int,int,INTERVAL_VECTOR &),
INTERVAL_VECTOR &Domain,
int M,
double epsilon,double epsilonf,
double *z,double delta,double mindelta,double mindz,
INTERVAL &Rangez,
int sens,
MATRIX &BRANCH,int *NBBRANCH)
The arguments are the same than for the previous procedure except for:
- Domain: the range for the m variable in which we will
look for solutions of the system,
- M is the maximum number of boxes which may be
stored (see the note 2.3.4.5)
- mindz: the accuracy
with which the starting point for the branches will be determined: if
the value of the parameter at which the branches will start is
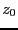 ,
then the system has no solution for
,
then the system has no solution for 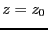 -mindz. This is done
by using a bisection on the parameter: if at
-mindz. This is done
by using a bisection on the parameter: if at 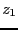 the system has no
solution and has a positive number of solution at
the system has no
solution and has a positive number of solution at 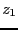 +delta,
then we will solve the system for
+delta,
then we will solve the system for 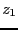 +delta/2. At each time we
will store the value
+delta/2. At each time we
will store the value 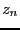 of the parameter for which there is no solution
of the system and the value
of the parameter for which there is no solution
of the system and the value 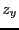 for which we have solutions and we
will stop the bisection on the parameter as soon as
for which we have solutions and we
will stop the bisection on the parameter as soon as 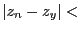 mindz.
mindz.
To determine the starting points of the branches this procedure uses the
solving procedure with the Hessian (see section 2.5). As
soon as initial valid solutions are
found the ALIAS_Start_Continuation procedure is called until
either a bound of the
parameter range is reached, or a singularity occur. In the later case the
solving procedure is called with an increased value for the
parameter. This algorithm cannot find isolated points and may miss
branches (see next section).
There is also another version of this program where you indicate just
before Domain the solutions which have already been found. The
syntax is
INTERVAL_MATRIX (* IntervalHessian)(int,int,INTERVAL_VECTOR &),
int NUM,
INTERVAL_MATRIX &Solutions,
INTERVAL_VECTOR &Domain
The return code for these procedures are:
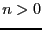 : the number of branches found by the algorithm
: the number of branches found by the algorithm
- -1: no initial point have been found
- -10: Newton algorithm has failed (should not occur)
- -20: sens is not 1 or -1
- -30: delta or mindelta is negative
Finding the initial starting point with the accuracy
mindz may be computer intensive.
Hence the integer global variable
ALIAS_Allow_Backtrack
enable to disable this process if it is set to 0 (its default value is
1): in that case as soon as starting points have been found (hence at
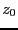 +
+  delta) we will start following the branches.
delta) we will start following the branches.
In fact these procedures are special occurrences of another ALIAS
procedure which has another argument right after the Hessian
argument. Assume for example that you are considering a system which
has one equation written as:
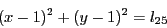
where 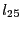 is the parameter of the system and
is the parameter of the system and 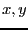 the
unknowns. When using the continuation method we have to define
ranges for these unknowns in order to be able to solve the system of
equations. Up to now we have indicated bounds that are constants but
for the equation example it will be interesting to be able to specify
that these bounds may change according to the value for the
parameter using a
simplification procedure.
In our example
clearly
the
unknowns. When using the continuation method we have to define
ranges for these unknowns in order to be able to solve the system of
equations. Up to now we have indicated bounds that are constants but
for the equation example it will be interesting to be able to specify
that these bounds may change according to the value for the
parameter using a
simplification procedure.
In our example
clearly 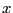 and
and 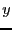 cannot exceed
cannot exceed 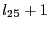 and
cannot be lower than
and
cannot be lower than 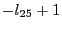 (this is an application of the
concept of
2B-consistency, see section 2.17).
Hence we may specify right after the
Hessian argument the name of a procedure, for example Range,
that is able to update
the bounds on the unknowns according to the value of the parameter (or
any other variable that may play a role). The syntax of the procedure
Range
is:
(this is an application of the
concept of
2B-consistency, see section 2.17).
Hence we may specify right after the
Hessian argument the name of a procedure, for example Range,
that is able to update
the bounds on the unknowns according to the value of the parameter (or
any other variable that may play a role). The syntax of the procedure
Range
is:
INTERVAL_VECTOR Range(double z, INTERVAL_VECTOR &Variable)
where z is parameter value and Variable the current set of ranges
for the unknowns. This procedure must return a set of ranges for the
unknowns (be careful to check that the returned ranges are included in
the initial ranges).
Note also that the ALIAS-Maple package offers a procedure that
uses the method described in section 2.14 for finding
the initial starting points of the branches: this method is efficient
if the equations include linear terms in the unknowns.




Next: Missed branches
Up: Implementation
Previous: Procedure for following branches
Contents
Jean-Pierre Merlet
2012-12-20
![]() +
+ ![]() delta) we will start following the branches.
delta) we will start following the branches.