



Next: Continuation for one dimensional
Up: Examples
Previous: Example 1
Contents
Consider the problem of finding the coordinates 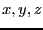 of a point
that lie on the surface
of a point
that lie on the surface
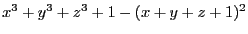 , is inside the
sphere centered at (-1,-1,0) of radius 1 and is the closest possible
to the center of this sphere, with the constraint that
, is inside the
sphere centered at (-1,-1,0) of radius 1 and is the closest possible
to the center of this sphere, with the constraint that 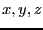 lie in the range [-2,2]. Thus we have:
lie in the range [-2,2]. Thus we have:
With epsilonf=0.0001 we find out that the point is located at
at (-0.747,-0.747,0.086059) which is well inside the sphere and that
the minimal distance is 0.13529.
We may also compute the minimal distance not to a point but to a line segment,
for example
defined by
![$x \in [0.9,1.1]$](img761.png) ,
, 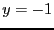 ,
, 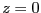 . In that case the optimum
function in the
evaluation procedure may be defined as:
. In that case the optimum
function in the
evaluation procedure may be defined as:
Sqr(x+INTERVAL(0.9,1.1))+Sqr(y+1)+Sqr(z)
and with epsilonf=0.0001 the algorithm will return that the
minimal distance lie in the range [0.0907,0.1925].
Jean-Pierre Merlet
2012-12-20
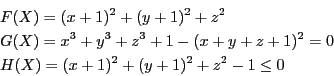
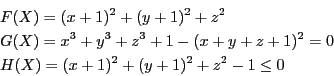
![]() ,
, ![]() ,
, ![]() . In that case the optimum
function in the
evaluation procedure may be defined as:
. In that case the optimum
function in the
evaluation procedure may be defined as: