



Next: Return code
Up: Implementation
Previous: Dealing with inequalities on
Contents
The optimization
method is implemented as:
int Minimize_Maximize_Gradient(int m,int n,
INTEGER_VECTOR &Type_Eq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int,INTERVAL_VECTOR &),
INTERVAL_VECTOR & TheDomain,
int Iteration,int Order,
double epsilon,double epsilonf,double epsilone,
int Func_Has_Interval,
INTERVAL Optimum,
INTERVAL_MATRIX & Solution,
int (* Simp_Proc)(INTERVAL_VECTOR &));
the arguments being:
- m: number of unknowns
- n: number of equations, see the note 2.3.4.1
- Type_Eq: type of the equations:
- Type_Eq(i)=-1 if equation i is a constraint
equation of type
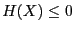
- Type_Eq(i)=0 if equation i is a constraint
equation of type
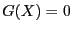
- Type_Eq(i)=1 if equation i is a constraint
equation of type
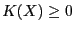
- Type_Eq(i)=-2 if equation i is the optimum
function to be minimized
- Type_Eq(i)=2 if equation i is the optimum
function to be maximized
- Type_Eq(i)=10 if equation i is the optimum
function for which is sought the minimum and maximum
- IntervalFunction: a function which return the interval
vector evaluation of the equations, see the note 2.3.4.3. This
function must be written in a similar manner than for the general
solving procedures.
- Gradient: a function which return the interval evaluation
of the gradient of the equations, see the note 2.4.2.2.
This
function must be written in a similar manner than for the general
solving procedures with the additional constraint that the
function to be minimized of maximized must be the last one.
- TheDomain: box in which we are looking for
the extremum of the optimum function
- Iteration: the number of boxes that may be
stored
- Order: a flag describing which order is used to store the
new boxes, see the note 8.3.4
- epsilon: the maximal width of the solution intervals but
not used. Should be set to 0.
- epsilonf: the maximal error for the equality
constraints. If the
problem has constraint of type
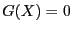 then a solution will verify
then a solution will verify
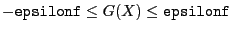
- epsilone: the maximal error on the extremum value.
If the extremum of the function is
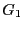 and the procedure
returns the value
and the procedure
returns the value 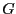 , then a minimum will verify
, then a minimum will verify
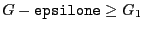 and a maximum
and a maximum
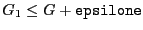 .
.
- Func_Has_Interval: 1 if the optimum function has
interval coefficients, 0 otherwise
- Optimum: an interval which contain the extremum value of
the optimum function
- Solution: an interval matrix of size at least (2,m)
which will contained the values of
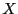 for which the extremum are
obtained
for which the extremum are
obtained
- Simp_Proc: an optional parameter which is a
simplification
procedure that may be provided by the user. It takes as input a box
 and may:
and may:
- either returns in
 a box with lower width than the initial
a box with lower width than the initial
 and a return code 0 or 1
and a return code 0 or 1
- or indicates that there is no solution to the
optimization problem in the current box, in which case the procedure
returns -1
Thus to minimize a function you have to set its Type_Eq to -2
and to maximize it to set its Type_Eq to 2.
Remember that you may use the 3B method to improve the efficiency of
this algorithm (see section 2.3.2).
Note also that a convenient way to write the IntervalFunction
and Gradient
procedures is to use the possibilities offered by ALIAS-Maple
(see the ALIAS-Maple manual).




Next: Return code
Up: Implementation
Previous: Dealing with inequalities on
Contents
Jean-Pierre Merlet
2012-12-20
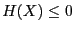
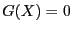
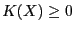
 a box with lower width than the initial
a box with lower width than the initial
 and a return code 0 or 1
and a return code 0 or 1