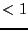Next: Characteristic polynomial
Up: Regularity of matrix with
Previous: Mathematical background
Contents
A regularity test based on this approach is implemented as:
int ALIAS_Check_Regularity_Linear_Matrix(int DimA,
INTERVAL_VECTOR (* Func)(int l1, int l2,INTERVAL_VECTOR & v_IS),
int (* A_Cond)(int dimA,
INTERVAL_VECTOR (* Func1)(int l1, int l2,INTERVAL_VECTOR &v_IS),
INTERVAL_VECTOR & v_IS,INTERVAL_MATRIX &A),
int Row_Or_Column,
int Context,
INTEGER_MATRIX &Implication_Var,
int Use_Rohn,
INTERVAL_VECTOR &Domain)
where
- Row_Or_Column: 1 if the row of the matrix are used, 2 if
the columns are used
- Context: is used to determine if this procedure is used
according to the following rules (see section 7.4 for the
meaning of the flag Simp_in_Cond):
- always used if 100 or if Context is equal to Simp_in_Cond
- not used if Context lie in [-2,2]
- not used if Context=3 and Simp_in_Cond
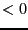
- not used if Context=4 and Simp_in_Cond
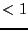
- not used if Context=5 and Simp_in_Cond is
not 0 or 1
- not used if Context=6 and Simp_in_Cond is
not 0 or 2
- Implication_Var: an integer matrix of dimension DimA
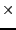
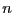 , where
, where 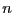 is the number of unknowns. If this matrix has
a 1 at row
is the number of unknowns. If this matrix has
a 1 at row 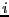 , column
, column 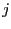 , then the unknown
, then the unknown 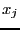 appear linearly in
some elements of row
appear linearly in
some elements of row 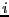 (or column
(or column 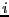 ) of the matrix
) of the matrix 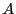
- Use_Rohn: 1 if the Rohn consistency test is used to check
that a matrix in
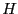 has a constant sign
has a constant sign
- Domain: the ranges for the input parameters
This procedure return -1 if all elements of 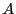 are regular, 0
otherwise
are regular, 0
otherwise




Next: Characteristic polynomial
Up: Regularity of matrix with
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20