



Next: Matrix inverse
Up: Calculating determinant
Previous: Scalar and interval matrix
Contents
Polynomial matrix
A polynomial matrix is assumed is assumed here to be a matrix whose
elements are univariate polynomial in the same variable. The
determinant of such matrix (which is a polynomial) may be computed
with the procedure
int Determinant_Characteristic(POLYNOMIAL_MATRIX A,
INTERVAL_VECTOR &Coeff)
where
- A: a POLYNOMIAL_MATRIX structure which describes
the polynomial matrix. This structure is composed of
- dim: the dimension of the matrix
- Coeff: an interval vector with indicates the
coefficients of the polynomial in the matrix, row by row
- Order: an integer matrix. m=Order(i,j)
indicates that the element at the
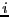 -th row and
-th row and 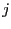 -th column has
coefficients Coeff(l) to Coeff(m) where l is Coeff(i,j-1)+1 if j is greater than 1, Coeff(i-1,dim)
otherwise. Hence Order(1,1)=3 indicate that the first elements
has as coefficient Coeff(1), Coeff(2), Coeff(3) and hence is a
second order polynomial
-th column has
coefficients Coeff(l) to Coeff(m) where l is Coeff(i,j-1)+1 if j is greater than 1, Coeff(i-1,dim)
otherwise. Hence Order(1,1)=3 indicate that the first elements
has as coefficient Coeff(1), Coeff(2), Coeff(3) and hence is a
second order polynomial
- Coeff: the coefficients of the determinant polynomial
Note that this procedure is safe: even for a scalar matrix the
coefficients of the determinant
will always include the coefficient of the exact determinant.




Next: Matrix inverse
Up: Calculating determinant
Previous: Scalar and interval matrix
Contents
Jean-Pierre Merlet
2012-12-20
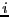 -th row and
-th row and 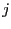 -th column has
coefficients Coeff(l) to Coeff(m) where l is Coeff(i,j-1)+1 if j is greater than 1, Coeff(i-1,dim)
otherwise. Hence Order(1,1)=3 indicate that the first elements
has as coefficient Coeff(1), Coeff(2), Coeff(3) and hence is a
second order polynomial
-th column has
coefficients Coeff(l) to Coeff(m) where l is Coeff(i,j-1)+1 if j is greater than 1, Coeff(i-1,dim)
otherwise. Hence Order(1,1)=3 indicate that the first elements
has as coefficient Coeff(1), Coeff(2), Coeff(3) and hence is a
second order polynomial