



Next: Implementation
Up: Cassini ovals
Previous: Cassini ovals
Contents
The Cassini ovals are another method to determine a bound for the
eigenvalues of a matrix.
Let 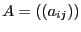 and the Cassini ovals defined as the set of
and the Cassini ovals defined as the set of 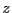 such that:
such that:
Column based Cassini ovals may also be defined.
The roots of the characteristic polynomial are enclosed in the union of
the row-based and column-based 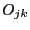 . Although more complicate to
calculate the bounds obtained with the Cassini ovals are usually
tighter than the bounds obtained with the Gerschgorin circles.
. Although more complicate to
calculate the bounds obtained with the Cassini ovals are usually
tighter than the bounds obtained with the Gerschgorin circles.
Jean-Pierre Merlet
2012-12-20