



Next: Implementation
Up: Gerschgorin circles
Previous: Gerschgorin circles
Contents
Let 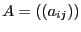 and the Gerschgorin circles defined as the set of
and the Gerschgorin circles defined as the set of
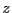 such that:
such that:
The roots of the characteristic polynomial are enclosed in the union of
the 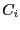 . Furthermore if a circle has no intersection with the other
circles, then this circle contains one root of the polynomial. This
allow for a fast determination of bounds for the real roots of the
polynomial.
. Furthermore if a circle has no intersection with the other
circles, then this circle contains one root of the polynomial. This
allow for a fast determination of bounds for the real roots of the
polynomial.
Jean-Pierre Merlet
2012-12-20