Implementation

This procedure determines the number of real roots of an univariate polynomial in a given interval. It is implemented as:

 
int Sturm_Interval(int Degree,VECTOR &Coeff,INTERVAL &In);
int Sturm_Interval(int Degree,INTEGER_VECTOR &Coeff,INTERVAL &In);

• Degree: degree of the polynomial
• Coeff: the Degree+1 coefficients of the polynomial in increasing degree, either real or integers
• In: the interval in which we are looking for the number of roots

This procedure returns 0 or a positive number on success, this number being the number of roots of the polynomial in the interval. A return code of -1 means that either the polynomial is equal to 0, is equal to 0 at one of the extremity of the interval or has multiple roots. However Sturm method is sensitive to numerical rounding errors. For high degree polynomial it may be better to use the "safer" procedure:

 
int Sturm_Safe_Interval(int Degree,VECTOR &Coeff,INTERVAL &In,INTERVAL &NbRoot);

which returns 1 in case of success and an interval NbRoot which contain the number of roots. If NbRoot=[a,b], then if a =b the number of roots is a and if a 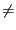$\not=$ b the number of roots is lower than b. Another safe procedure can be used if the coefficients are integers and the interval is also defined by integer numbers:

 
int Sturm_Interval(int Degree,INTEGER_VECTOR &Coeff,int Inf,int Sup);

This procedure will return -1 if all the coefficients are 0 and -2 if at some point of the process an integer larger than the largest machine integer is encountered (Not yet implemented).