



Next: Example
Up: Budan-Fourier method
Previous: Mathematical background
Contents
This procedure is used to determine the number of real roots in a
given interval, up to an even number.
The syntax of the procedure is:
INT Budan_Fourier_Interval(int Degree,VECTOR &Coeff,INTERVAL In)
INT Budan_Fourier_Interval(int Degree,INTEGER_VECTOR &Coeff,INTERVAL In)
with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the
polynomial in increasing degree, which may be REAL or INT
- In: the interval in which we are looking for the number of
roots
If this procedure returns the integer 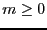 , then the number of real
roots in In is
, then the number of real
roots in In is 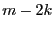 with
with ![$k\in[0,m/2]$](img582.png) .
A negative returns code indicate a failure of the algorithm:
.
A negative returns code indicate a failure of the algorithm:
- -1:
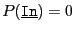
- -2:
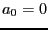 , the polynomial may be factored
, the polynomial may be factored
- -3:
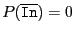
This procedure may be used with polynomial whose coefficients are
intervals. The syntax is:
INT Budan_Fourier_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL In,int *Confidence)
where Confidence is a quality index for the result:
- 1: the result is exact, so if
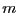 is the return code of the
algorithm the number of reals roots of the interval polynomial is
is the return code of the
algorithm the number of reals roots of the interval polynomial is
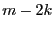 with
with ![$k\in[0,m/2]$](img582.png)
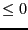 : if
: if 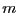 is the return code of the
algorithm the number of reals roots of the interval polynomial is
is the return code of the
algorithm the number of reals roots of the interval polynomial is 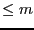
Due to rounding errors incorrect results may be returned by the
previous procedures. A safer procedure is:
INT Budan_Fourier_Safe_Interval(int Degree,VECTOR &Coeff,
INTERVAL In,INTERVAL &NbRoot);
The procedure returns 1 in case of success and an interval for the
number of roots. If NbRoot=[a,b], then if a =b the number of
roots is either a,a-2,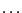 and if a
and if a 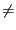 b the number of roots
is lower than b.
If "safe" value of the coefficients have been pre-computed you may
use:
b the number of roots
is lower than b.
If "safe" value of the coefficients have been pre-computed you may
use:
INT Budan_Fourier_Fast_Safe_Interval(int Degree,INTERVAL_VECTOR &Coeff,
INTERVAL In,INTERVAL &NbRoot);
Another safe procedure is:
INT Budan_Fourier_Interval(int Degree,INTEGER_VECTOR &Coeff,int Inf,int Sup)
where the coefficients and the bounds are integers.




Next: Example
Up: Budan-Fourier method
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20