



Next: Maximum number of real
Up: Bounds on the product
Previous: Mathematical background
Contents
Let 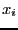 be the
be the  roots (either complex or real) of
a polynomial of degree
roots (either complex or real) of
a polynomial of degree  . Let
. Let 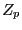 be:
be:
This procedure enable to compute the  elements
elements
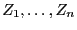 (
(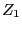 is the sum of the roots,
is the sum of the roots, 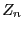 the product of the roots).
The syntax is:
the product of the roots).
The syntax is:
VECTOR ProdN_Polynomial_Interval(int Degree,VECTOR &Coeff)
with:
- Degree: degree of the polynomial
- Coeff: coefficients of the polynomial ordered along
increasing degree
This procedure returns 0 if the leading coefficient is equal to 0, 1
otherwise.
There is an equivalent procedure for interval polynomial:
INTERVAL_VECTOR ProdN_Polynomial_Interval(int Degree,INTERVAL_VECTOR &Coeff)
which returns intervals including the 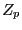 .
This procedure returns 0 if 0 is included in the leading interval.
.
This procedure returns 0 if 0 is included in the leading interval.
Jean-Pierre Merlet
2012-12-20