Implementation

This procedure is able to give an upper bound on the absolute value of the roots as soon as all the roots are real (this is checked using Huat theorem, section 5.5.4). The syntax is:

 
int Newton_Second_Bound_Interval(int Degree,VECTOR &Coeff,double *bound);

with:

• Degree: degree of the polynomial
• Coeff: the Degree+1 coefficients of the polynomial in increasing degree
• bound: upper bound on the absolute value of the roots

The procedure returns 0 if Degree=0 or Coeff(Degree+1)=0, 1 otherwise. We may also compute a lower bound on the absolute value of the root by using:

 
int Newton_Second_Bound_Inverse_Interval(int Degree,VECTOR &Coeff,double *bound);

An upper and lower bound on the absolute value of the roots may be compute by:

 
int Newton_Second_Bound_Interval(int Degree,VECTOR &Coeff,INTERVAL &Bound);

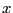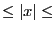In that case if Bound=[a,b] we have for all root $x$: a$\le \vert x\vert \le$ b.

Similar procedures exist for interval polynomial:

 
int Newton_Second_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound);
int Newton_Second_Bound_Inverse_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &Bound);
int Newton_Second_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,INTERVAL &L, INTERVAL &U);

where

• Bound: upper or lower bound on the absolute value of the root of the polynomials
• L,U: if L=[a,b] then the absolute value of the roots of any polynomial in the set is greater than a while some polynomial have root greater than b. Conversely if U=[a,b] the absolute value of the roots of any polynomial in the set is lower than b while some polynomial have root lower than a.