



Next: Implementation
Up: Newton method
Previous: Newton method
Contents
Let 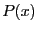 be an univariate polynomial of degree
be an univariate polynomial of degree  :
:
with 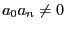 ,
, 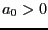 .
Newton theorem state that if it exists
.
Newton theorem state that if it exists 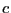 such that
such that 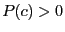 and
for all the
derivative
and
for all the
derivative 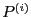 of
of  , with
, with ![$i \in [1,n]$](img530.png) , then
, then 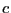 is an upper
bound of the positive roots of
is an upper
bound of the positive roots of  .
To find
.
To find 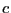 the following
scheme can be used:
the following
scheme can be used:
- let
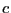 be such that
be such that
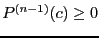
- let
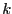 the smallest integer such that either
the smallest integer such that either 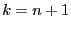 or
or 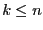 and
and
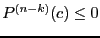
- if
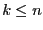 then substitute
then substitute 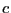 by
by 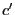 such that
such that
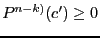 and go to 2
and go to 2
- return
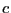
A consequence of Newton theorem is that the best bound cannot be
lower than 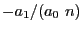 .
.
Jean-Pierre Merlet
2012-12-20