



Next: The 3B method
Up: Mathematical background
Previous: An alternative: the single
Contents
An interval will be considered as a solution for a function
of the system in the following cases:
- for equations the maximal diameter of the intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function contains 0 or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
- for inequalities
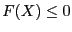 : the upper bound of
the interval evaluation of the
function is negative or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a negative lower bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
: the upper bound of
the interval evaluation of the
function is negative or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a negative lower bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
- for inequalities
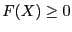 : the lower bound of
the interval evaluation of the
function is positive or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a positive upper bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
: the lower bound of
the interval evaluation of the
function is positive or the maximal diameter of the
intervals is less than
a given threshold epsilon and the corresponding interval
evaluation of the function has at least a positive upper bound or the corresponding interval
evaluation of the function has a diameter less than a given threshold
epsilonf and the interval contains 0
A solution of the system is defined as a box such that
the above conditions hold for each function of the system.
Note that for systems having interval coefficients (which are
indicated by setting the flag ALIAS_Func_Has_Interval to 1)
a solution of a system will be obtained only if the inequalities are
strictly verified.
Assume that two solutions
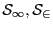 have been found
with the algorithm.
We will first consider the case where we have to solve a system of
have been found
with the algorithm.
We will first consider the case where we have to solve a system of  equations in
equations in  unknowns, possible with additional inequality
constraints.
First we will check with the Miranda theorem (see
section 3.1.5) if
unknowns, possible with additional inequality
constraints.
First we will check with the Miranda theorem (see
section 3.1.5) if
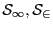 include one (or
more) solution(s). If both solutions are Miranda, then they will kept
as solutions. If one of them is Miranda and other one is not Miranda
we will consider the distance between the mid-point of
include one (or
more) solution(s). If both solutions are Miranda, then they will kept
as solutions. If one of them is Miranda and other one is not Miranda
we will consider the distance between the mid-point of
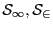 : if this distance is lower than a given threshold we will
keep as solution only the Miranda's one. If none of
: if this distance is lower than a given threshold we will
keep as solution only the Miranda's one. If none of
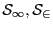 is Miranda we keep these solutions, provided that their distance
is greater than the threshold. Note that in that case these solutions
may disappear if a Miranda solution is found later on such that the
distance between these solutions and the Miranda's one is lower than
the threshold.
is Miranda we keep these solutions, provided that their distance
is greater than the threshold. Note that in that case these solutions
may disappear if a Miranda solution is found later on such that the
distance between these solutions and the Miranda's one is lower than
the threshold.
In the other case the solution will be ranked according the chosen
order and if a solution is at a distance from a solution with a better
ranking lower than the threshold, then this solution will be discarded.




Next: The 3B method
Up: Mathematical background
Previous: An alternative: the single
Contents
Jean-Pierre Merlet
2012-12-20
![]() have been found
with the algorithm.
We will first consider the case where we have to solve a system of
have been found
with the algorithm.
We will first consider the case where we have to solve a system of ![]() equations in
equations in ![]() unknowns, possible with additional inequality
constraints.
First we will check with the Miranda theorem (see
section 3.1.5) if
unknowns, possible with additional inequality
constraints.
First we will check with the Miranda theorem (see
section 3.1.5) if
![]() include one (or
more) solution(s). If both solutions are Miranda, then they will kept
as solutions. If one of them is Miranda and other one is not Miranda
we will consider the distance between the mid-point of
include one (or
more) solution(s). If both solutions are Miranda, then they will kept
as solutions. If one of them is Miranda and other one is not Miranda
we will consider the distance between the mid-point of
![]() : if this distance is lower than a given threshold we will
keep as solution only the Miranda's one. If none of
: if this distance is lower than a given threshold we will
keep as solution only the Miranda's one. If none of
![]() is Miranda we keep these solutions, provided that their distance
is greater than the threshold. Note that in that case these solutions
may disappear if a Miranda solution is found later on such that the
distance between these solutions and the Miranda's one is lower than
the threshold.
is Miranda we keep these solutions, provided that their distance
is greater than the threshold. Note that in that case these solutions
may disappear if a Miranda solution is found later on such that the
distance between these solutions and the Miranda's one is lower than
the threshold.