The Wright omega function

>    omega := proc(z) LambertW(exp(z)); end;

omega := proc (z) LambertW(exp(z)) end proc

>    normal(pmint(omega(x),x));

1/2*LambertW(exp(x))*(LambertW(exp(x))+2)

>    f := (1 + omega(x) * (2 + cos(omega(x)) * (x + omega(x)))) / (1 + omega(x)) / (x + omega(x));

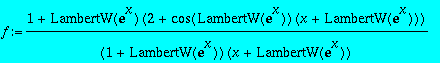
f := (1+LambertW(exp(x))*(2+cos(LambertW(exp(x)))*(x+LambertW(exp(x)))))/(1+LambertW(exp(x)))/(x+LambertW(exp(x)))

>    pmint(f,x);

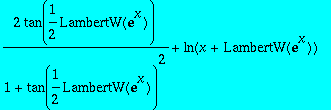
2*tan(1/2*LambertW(exp(x)))/(1+tan(1/2*LambertW(exp(x)))^2)+ln(x+LambertW(exp(x)))

This one is also beyond Maple

>    int(f,x);

int((1+LambertW(exp(x))*(2+cos(LambertW(exp(x)))*(x+LambertW(exp(x)))))/(1+LambertW(exp(x)))/(x+LambertW(exp(x))),x)

>   

>