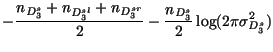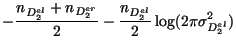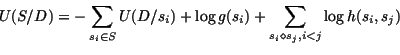

Next: Construction of a RJMCMC
Up: Roads Extraction using a
Previous: Stochastic model for a
Data term for the Candy model
Hypothesis tests :
H3 : we have three different regions
Figure 5:
Three region mask
|
|
Using a Gaussian assumption, the log of the likelihood function is :
H2 : we have two different
regions
Figure 6:
Two region mask
|
|
The log of the likelihood function :
H1 : the segment is in the middle of an homogeneous region
Figure 7:
One region mask
|
|
The log of the likelihood function :
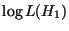 |
= |
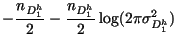 |
(16) |
|
The Total Energy for the Candy model
The conditional energy for a segment :
| UD(s) |
= |
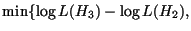 |
|
| |
|
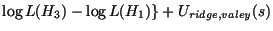 |
(17) |
Depending on the type of image, we may add to the conditional term :
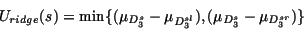 |
(18) |
or :
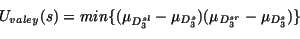 |
(19) |
The total energy becomes :
with :
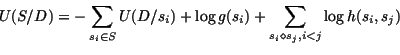 |
(21) |

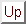

Next: Construction of a RJMCMC
Up: Roads Extraction using a
Previous: Stochastic model for a
Radu Stoica
2000-04-17
![\includegraphics[width=5cm]{/u/biotite/0/ariana/rstoica/DOCS99/FIGURES/trois_regions.eps}](img42.gif)