

An early paper presenting CYP can be found here.
Colouring is just a graphical way to indicate the structure of the proof. Internally CYP uses tag. When displaying its internal structure, it simply associates a colour to each tag. A tag indicates a region of the proof text and has a specific colour. The core structure has five different tags:
Property exp_pos:
Let x and y be two integers, if 0 < x, to prove 0 < x^y, we have three cases:
If 0 < y then x^1 <= x^y
If 0 = y then x^y = 1
If y < 0 then x^y = 1/(x^(-y))
Note that we have been using indentation only for legibility. The
system does not impose any formatting style.
Property exp_pos:
<p>Let x and y be two integers, if 0 < x, to prove 0 < x^y, we have three cases:
<p> If 0 < y then x^1 <= x^y </p>
<p> If 0 = y then x^y = 1 </p>
<p> If y < 0 then x^y = 1/(x^(-y))</p>
<p>
Property exp_pos:
<p>Let x and y be two integers, if 0 < x, to prove <c> 0 < x^y</c>, we have three cases:
<p> If 0 < y then <c>x^1 <= x^y</c></p>
<p> If 0 = y then <c>x^y = 1</c></p>
<p> If y < 0 then <c>x^y = 1/(x^(-y))</c></p>
<p>
Property exp_pos:
<p> Let x and y be two integers, if <h>0 < x</h>, to prove <c>0 < x^y </c>, we have three cases:
<p> If <h>0 < y</h> then <c>x^1 <= x^y</c></p>
<p> If <h>0 = y</h> then <c>x^y = 1</c></p>
<p> If <h>y < 0</h> then <c>x^1 = 1/(x^(-y))</c></p>
<p>
Property exp_pos:
<p> Let <v>x</v> and <v>y</v> be two integers, if <h>0 < x</h>, to prove <c>0 < x^y</c>, we have three cases:
<p> If <h>0 < y</h> then <c>x^1 <= x^y</c></p>
<p> If <h>0 = y</h> then <c>x^y = 1</c></p>
<p> If <h>y < 0</h> then <c>x^y = 1/(x^(-y))</c></p>
<p>
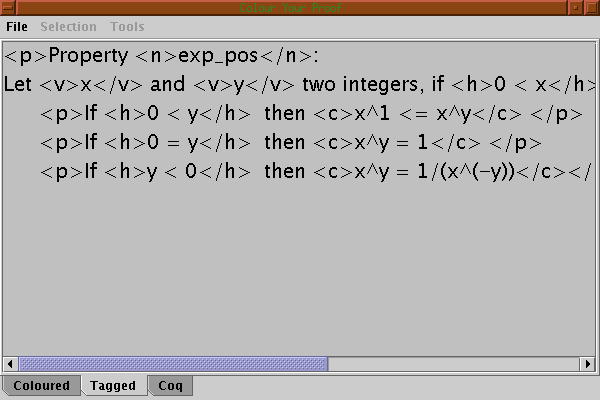
Property <n>exp_pos</n>:
<p> Let <v>x</v> and <v>y</v> be two integers, if <h>0 < x</h>, to prove <c>0 < x^y</c>, we have three cases:
<p> If <h>0 < y</h> then <c>x^1 <= x^y</c></p>
<p> If <h>0 = y</h> then <c>x^y = 1</c></p>
<p> If <h>y < 0</h> then <c>x^y = 1/(x^(-y))</c></p>
<p>
Removing all the tags, we get the coloured proof:
Property exp_pos:
Let x and y be two integers, if 0 < x , to prove 0 < x^y, we have three cases:
If 0 < y then x^1 <= x^y
If 0 = y then x^y = 1
If 0 > y then x^y = 1/(x^(-y))
Two extra tags have also be added for naming hypothesis and for justification
<h>0 < x <n>H</n></h>As sometimes it is necessary to have some extra characters between the value of the hypothesis and its name, a special tag f allows to indicate the formula of an assumption so for example we have:
<h><f>0 < x 0</f> (<n>H</n>) </h>
By theorems exp_inv and exp_rec, we have ...can be coloured as
<j>By theorems <n>exp_inv<n> and <n>exp_rec<n></j>, we have ...Furthermore it also is possible to make reference to assumptions by value instead of by name using the tag f :
<j>By <f>A and B</f></j>, we have ...
For the moment the interface can only be used to colour the proof text. No editing is permitted. The first step is then to load the proof we want to colour using the Open File button:
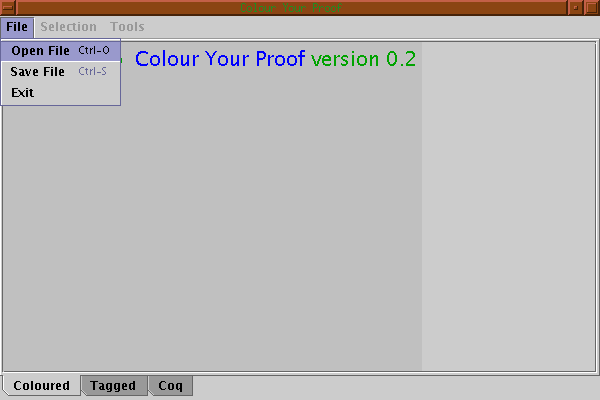
Let us suppose we load the uncoloured version of our previous example
Now to colour the conclusion of the main proof, we first need it to select the text of the conclusion with the mouse, then we need to select the Set as conclusion menu.
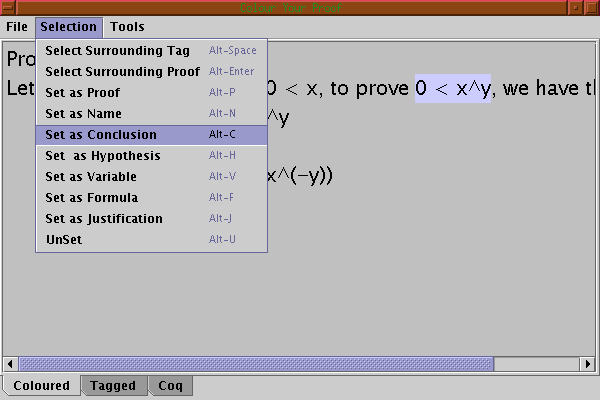
The conclusion is now in blue, it has been coloured.
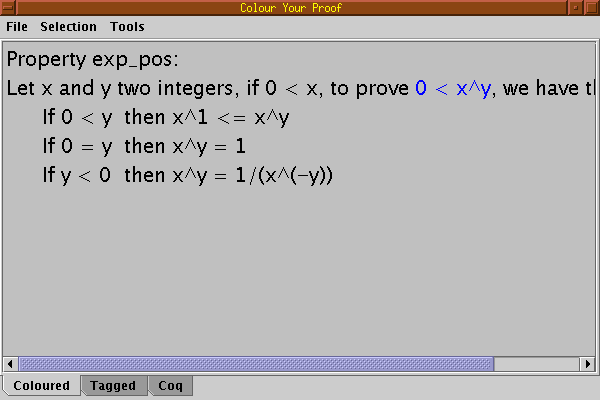
Colouring the whole like explained in the previous section gives the following result:
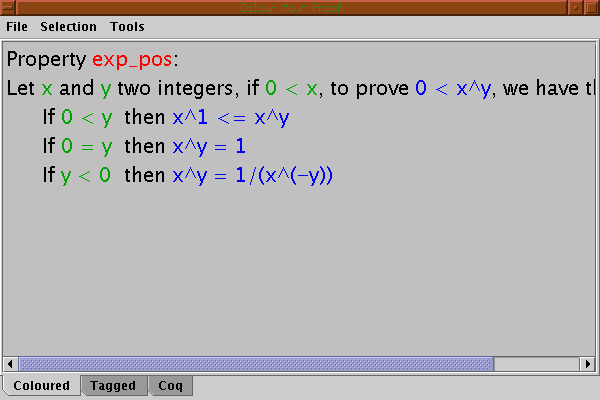
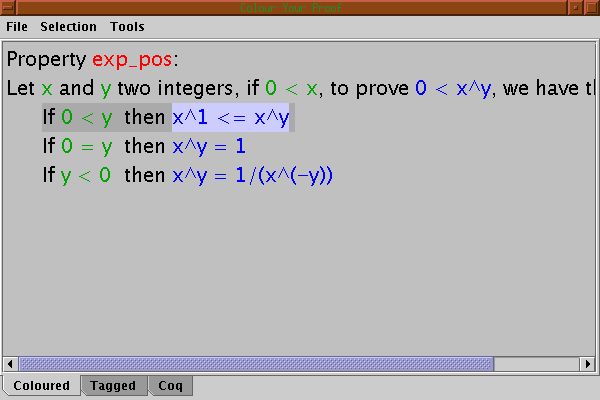
In the interface only proof tags are not coloured. As proofs can be nested, the colour of the main proof would hide the colours of the subproofs. For this reason. the interface only shows the immediate surrounding subproof of the current selection. For example, if we select the conclusion of the first subgoal we have:
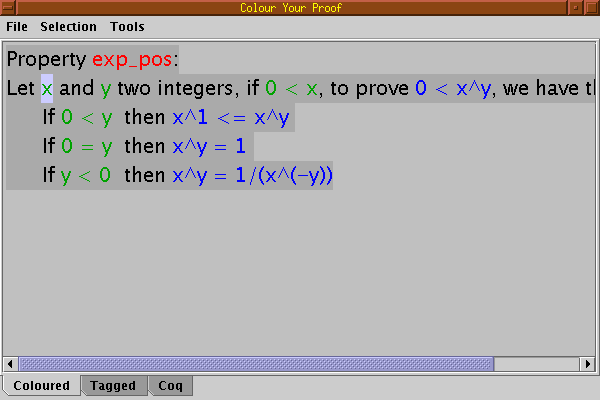
Selecting the first variable of the main proof gives:
At any time, it is possible to get the tagged version of the proof, selecting the tab Tagged
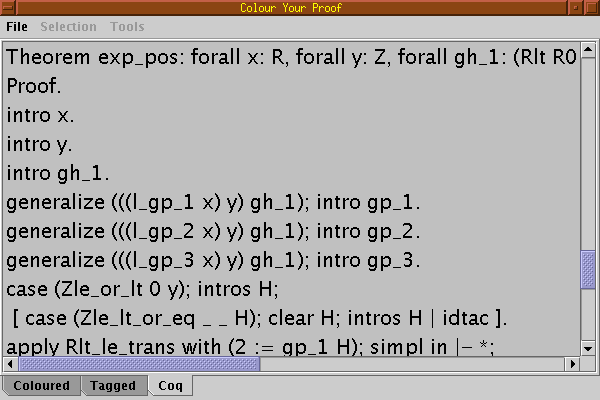
Once a proof is completely coloured, it is possible to generate the output for a particular prover selecting the last tab (here the Coq output):
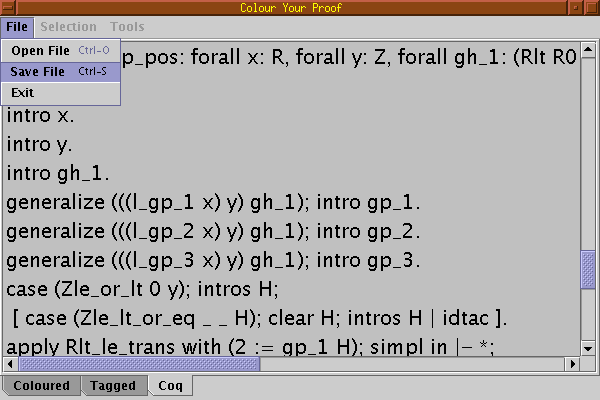
Any of this two formats can be saved on file:
java -jar cyp.jarHere are some examples. For more information on the command, read this.
The current implementation of CYP is written in Java. We are happy user of the ANTLR tool.