|
Théorème InvTrans. Énoncé :  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R) (Trans E (Inv E R)). (Trans E (Inv E R)).Proof : Considérons un ensemble E quelconque ; un terme R quelconque de type (Rel E) ; posons par hypothèse (Trans R E) (H) ; considérons trois éléments x, y, et z quelconques de E ; posons par hypothèse (Inv E R x y) (H1) et (Inv E R y z) (H2). En appliquant l'hypothèse H à z, y, x, H2 et H1 nous avons (R z x). Nous avons montré  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R)  x,y,z:E.(Inv E R x y) x,y,z:E.(Inv E R x y) (Inv E R y z) (Inv E R y z) (R z x). (R z x).Qed. |
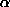
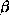
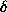 -conversion des types). Voyons par
la
-conversion des types). Voyons par
la