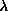 -terme
-terme| Retour | Sommaire | Suite |
 -terme
-terme Dans le Calcul des Construction tout se passe
autour de 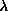 -termes. C'est le nom
donné aux définitions est aux preuves. Notre exemple n'y fait pas
exception. Voici un mini exemple de développement sur les
relations.
-termes. C'est le nom
donné aux définitions est aux preuves. Notre exemple n'y fait pas
exception. Voici un mini exemple de développement sur les
relations.
Definition Rel := 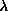 E:Set.E E:Set.E E E Prop. Prop.Definition Inv := 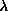 E:Set. E:Set.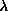 R:(Rel E). R:(Rel E).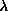 x,y:E.(R y x). x,y:E.(R y x).Definition Trans := 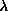 E:Set. E:Set.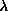 R:(Rel E). R:(Rel E). x,y,z:E.(R x y) x,y,z:E.(R x y) (R y z) (R y z) (R x z). (R x z).Definition InvTrans :  E:Set. E:Set. R:(Rel E).(Trans E R) R:(Rel E).(Trans E R) (Trans E (Inv E R)) = (Trans E (Inv E R)) =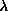 E:Set. E:Set.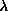 R:(Rel E). R:(Rel E).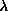 H:( H:( x,y,z:E.(R x y) x,y,z:E.(R x y) (R y z) (R y z) (R x z)). (R x z)).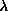 x,y,z:E. x,y,z:E.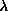 H0:(R y x). H0:(R y x).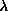 H1:(R z y).(H z y x H1 H0). H1:(R z y).(H z y x H1 H0). |
Ceci étant difficilement compréhensible sans une
bonne connaissance du 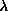 -calcul et
du Calcul des Constructions, nous allons tenter d'expliquer ces
instructions une à une. L'idée générale d'un tel développement
est de redéfinir petit à petit sous une forme formelle tout un
ensemble de notions mathématiques habituelles. On fait
correspondre à chacune de ces notions une constante au nom
explicite.
-calcul et
du Calcul des Constructions, nous allons tenter d'expliquer ces
instructions une à une. L'idée générale d'un tel développement
est de redéfinir petit à petit sous une forme formelle tout un
ensemble de notions mathématiques habituelles. On fait
correspondre à chacune de ces notions une constante au nom
explicite.
Les quelques lignes précédentes avaient pour but de définir cette preuve. Le système a maintenant vérifié qu'elle ne comporte aucune erreur. Nous nous avons maintenant la certitude que l'inverse d'une fonction transitive est transitive. Cependant, nous n'avons aucun document compréhensible pour en expliquer la raison. C'est ici que mon travail de thèse intervient. Il consiste à écrire un programme qui traduise ces quelques lignes en français. Je vais ici tacher de vous monter de quelle façon il procède. (Suite)
| Retour | Sommaire | Suite |