Next: About this document ...
CURRICULUM VITÆ
|
Heikel BATNINI
French nationality, born 1976, Nov. 14th, 1 child
Professional address
INRIA Sophia-Antipolis
Projet HEPHAISTOS
2004, Route des Lucioles. BP 93
06902 Sophia Antipolis. Cedex. France
Tel. office : (+33) 4.92.38.77.48
Fax : (+33) 4.92.38.76.43
e-mail : Heikel.Batnini@sophia.inria.fr
Web : http://www-sop.inria.fr/hephaistos/batnini
|
|
[scale=1.8]heikel.jpg
Personal address
28, rue Abbé Grégoire
06000 Nice
Tel. home : (+33) 4.93.88.06.54
e-mail : batninih@wanadoo.fr
|
Education
Since 2002
PhD in Computer
Science University of Nice
2001 - 2002 D.E.A. in Computer Science
(w/ honors, ranked 1st/19) University of Nice
2000 - 2001 Master's degree in Computer
Science (w/ honors, ranked 5th/69) University of Nice
1999 - 2000 Bachelor's degree in Computer Science University of Nice
1996 - 1999 Bachelor's degree in Mathematics University of Nice
Skills
- Areas of expertise : Constraint programming,
interval analysis, numerical optimization
- Operating Systems : Linux, Windows, MacOs
- Programming Languages : C, C++, Java, Scheme, Maple,
Mupad, Scilab, Bigloo, Pascal, Perl, Ada, Tcl/Tk, Shell, HTML, SQL, UML
- Other skills : Computational geometry, algebraic methods, grid computing, network programming, concurrent
programming, algorithmic, artificial intelligence, complexity, langage theory, automata theory,
graph theory, logic, data bases, cryptology, compilation, object
oriented design, software engineering, computer vision,
3D engines
- Languages spoken : French (native), English (good),
Spanish and Arab (some notions).
Professional Experience
Since Oct. 2002 PhD in
Computer Science
University of Nice
(Defense in November 2005) HEPHAISTOS Project
Director : Michel Rueher I.3.S./I.N.R.I.A./CERTIS
Title : Global Constraints for Numerical Constraint
Satisfaction Problems.
Keywords : Constraint programming, interval
analysis, search techniques, consistency techniques, global constraints, distance constraints (applications in robotics, molecular biochemistry)
Jan. 2002 - Sept. 2002 Research
internship University of Nice
(D.E.A.1 of Computer Science) HEPHAISTOS Project
Director : Michel Rueher, Claude Michel I.3.S./I.N.R.I.A./CERTIS
Title : Global Constraints for Solving
Euclidean Distance Constraints.
Keywords : Constraint programming, interval
analysis, search techniques, consistency techniques, global constraints, distance constraints (applications in robotics, molecular biochemistry)
Avr. 2001 - Sept. 2001
Research internship
NARVAL/SUMARE Project
(within my Master's degree of Computer Science) I.3.S./University of Nice
Advisor : Maria Joao Rendas, Stefan Rolfes and
Jean-Pierre Folcher.
Title : Automatic mosaïc creation from ocean floor images.
Keywords : Computer vision
Nov. 2000 - Mar. 2001
Engineer internship
NARVAL/SUMARE Project
Advisor : Maria Joao Rendas, Stefan Rolfes and
Jean-Pierre Folcher. I.3.S./University of Nice
Title : Development of a GUI for the
guidance of a submarine robot.
Keywords : Computer vision
Teaching
Oct. 2002 - Sept. 2005 Computer Science Teacher
Computer Science Department, University of
Nice
- Topics : Algorithmic and programming in Java
(65h), Advanced algorithmic (99h), Languages and Automata (26h),
Operating Systems (26h), Data Bases (24h), Image processing (19h).
- Miscellaneous : Involved in the preparation of practical courses
material and examining questions. Responsible
of the practical course of Algorithmic for the 2nd year of BSc (2002-2004).
Director of 4 BSc end year projects (2005) and member of
the evaluation commitee (2004 and 2005).
Oct. 2001 - Sept. 2002 Computer Science Lecturer
Computer Science Department, University of Nice
- Topics : Algorithmic and programming in Java (96h),
Advanced algorithmic (48h), responsible of the practical courses
(Scheme).
Miscellaneous
Part-time Jobs (full finance of my studies) :
Jan. 1999 - Sept. 2000
Mathematics Teacher (Home study courses)
Acadomia
Mar. 2000 - Jun. 2000
Cashier assistant
Auchan supermarket
Jul. 1996 - Avr. 2000 Pizza Deliverer/Receptionist/Pizzaïolo/Manager
Mister Pizza
Research
Since Oct. 2002 PhD Thesis
University of Nice
Director : Michel Rueher HEPHAISTOS Project
Title : Global Constraints for Numerical Constraint
Satisfaction Problems. I.3.S./I.N.R.I.A./CERTIS
Expected graduation date : November 2005
The main part of our works concerns systems of distance equations and
inequations. Such distance constraints can be defined as follows:
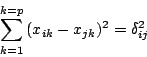
where 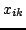 is the
is the 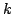 -th coordinate of the point
-th coordinate of the point 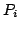 in the
euclidian space of dimension
in the
euclidian space of dimension 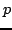 , and
, and 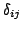 is a positive
real value.
More generally, this value can be given by
an interval:
is a positive
real value.
More generally, this value can be given by
an interval:
![$\delta_{ij} \in [\underline{\delta_{ij}},\overline{\delta_{ij}}]$](img7.png) ,
where
,
where
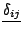 (resp.
(resp.
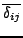 ) stands for the minimal (resp. maximal)
euclidian distance between
) stands for the minimal (resp. maximal)
euclidian distance between 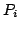 and
and 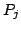 .
Finding all the roots of such systems is NP-complete.
These constraints are widely used in many
applications ranging from robot kinematics to chemistry.
One branch of computational molecular biology study the automation of
structure determination for instance for drug design.
The problem of molecular conformation is equivalent
to finding the forward kinematics of robots, which is crucial
for optimal design.
Several computer assisted design softwares uses
a representation by geometric constraints and particularly distance
constraints.
Classical methods for solving numerical constraints are based on
local consistencies like 2B-consistency or
Box-consistency.
The drawback of these methods comes from the fact that constraints are
handled independently and in a blind way i.e., local
consistencies do not take advantage of the specific semantic
properties of distance constraints. In the purpose of distance
constraints solving, we explored 3 different approaches :
introduction of redundant constraints, a global
pruning method and a specific splitting strategy :
.
Finding all the roots of such systems is NP-complete.
These constraints are widely used in many
applications ranging from robot kinematics to chemistry.
One branch of computational molecular biology study the automation of
structure determination for instance for drug design.
The problem of molecular conformation is equivalent
to finding the forward kinematics of robots, which is crucial
for optimal design.
Several computer assisted design softwares uses
a representation by geometric constraints and particularly distance
constraints.
Classical methods for solving numerical constraints are based on
local consistencies like 2B-consistency or
Box-consistency.
The drawback of these methods comes from the fact that constraints are
handled independently and in a blind way i.e., local
consistencies do not take advantage of the specific semantic
properties of distance constraints. In the purpose of distance
constraints solving, we explored 3 different approaches :
introduction of redundant constraints, a global
pruning method and a specific splitting strategy :
- Introduction of Redundant Constraints : In [7], we
used a algorithm based on Floyd's shortest path algorithm to
compute intervals for the missing distances; the bounds of these
intervals satisfy distance triangular inequalities.
Then, we introduced additional points (barycenter of triangles) to
reinforce the pruning achieved by local consistencies.
- A Global Filtering Algorithm : In [3], we introduced a global filtering algorithm for handling
systems of distance relations. This new method, named
QuadDist, is derived from Quad, a global filtering
algorithm for handling systems of quadratic equations and
inequations. Quad computes a tight linear relaxation of the terms of the
quadratic equations and uses the simplex algorithm to reduce the
domains of the variables.
We proposed a new linear approximation for handling distance relations.
The key point of this new method is that the approximations are not
generated for each quadratic terms but for each distance constraint.
Thus, QuadDist defines a tighter approximation than Quad
without the need to generate any additional variables.
Experimental results proved that QuadDist outperforms
Quad on systems of distance constraints.
- A Specific Search Algorithm : In [4,5,6], we proposed a strategy, named SDD(Semantic
Domain Decomposition), for choosing splitting points in the domains of
the variables. These choices are defined by the monotonicity and convexity properties
of the distance constraints and by the distribution of the local solutions
in the space. Experimental results show that this heuristic improves the
performances of the classical branching algorithm.
More recently, this specific search algorithm was extended for
handling more general CSPs. In [1,2], we proposed a new splitting
strategy for branch and bound algorithms based on consistency
techniques :
- A Search Strategy for Consistency Techniques :
Classical methods for solving numerical CSPs are based on a branch and
prune algorithm, a dichotomic enumeration process interleaved with a
consistency filtering algorithm.
In many interval solvers, the pruning step is based on local consistencies
(Hull-Consistency, Box-consistency) or partial consistencies
(
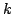 B-consistencies, Bound-consistency).
The associated pruning algorithms compute
numerous data required to identify gaps within some domains, i.e. inconsistent
intervals strictly included in the domain.
However, these gaps are only used to compute the smallest approximation
of the box enclosing all the solutions.
In [6,7], we introduced a search strategy, named T1cmssnnMindTheGaps,
that takes advantage of the gaps identified during the filtering process.
Gaps are collected with a negligible overhead, and are used to select
the splitting direction as well as to define relevant cutting points within the domain.
Splitting the domain by removing such gaps definitely reduces the
search space. It also helps to discard some redundant solutions and
helps the search algorithm to isolate different solutions.
First experimental results shows that
T1cmssnnMindTheGaps significantly improves performances of
the search process.
B-consistencies, Bound-consistency).
The associated pruning algorithms compute
numerous data required to identify gaps within some domains, i.e. inconsistent
intervals strictly included in the domain.
However, these gaps are only used to compute the smallest approximation
of the box enclosing all the solutions.
In [6,7], we introduced a search strategy, named T1cmssnnMindTheGaps,
that takes advantage of the gaps identified during the filtering process.
Gaps are collected with a negligible overhead, and are used to select
the splitting direction as well as to define relevant cutting points within the domain.
Splitting the domain by removing such gaps definitely reduces the
search space. It also helps to discard some redundant solutions and
helps the search algorithm to isolate different solutions.
First experimental results shows that
T1cmssnnMindTheGaps significantly improves performances of
the search process.
References :
- [1]
- H. Batnini, C. Michel, M.Rueher. MindTheGaps : A
New Splitting Strategy for Consistency Techniques.
To appear in Proceedings of CP'05. 11th International Conference on Principles and Practice of Constraint Programming.
October 2005. Barcelona. Spain.
- [2]
- H. Batnini, M.Rueher. Une Stratégie de Recherche Basée sur la
Topologie des CSPs continus.
Actes JFPC'05. 1st French Conference on Constraint Programming.
June 2005. Lens. France.
- [3]
- H. Batnini, M.Rueher. QuadDist: Filtrage Global pour les Contraintes de Distance
Actes JNPC'04. 10th French conference on NP-complete
problems solving. June 2004. Angers. France.
- [4]
- H. Batnini, M.Rueher. Décomposition sémantique pour la résolution de systèmes d'équations de distances.
JEDAI. Electronic Journal of Artifical Intelligence. Special track JNPC 2003.
- [5]
- H. Batnini, M.Rueher. Semantic Decomposition for Solving Distance Constraints.
Proceedings of CP'03. 9th International Conference on Principles and Practice of Constraint Programming.
September 2003. Kinsale, Co. Cork, Ireland.
- [6]
- H. Batnini, M.Rueher. Filtrage Local par Décomposition de CSP Continus
Proceedings of JNPC'03. 9th French conference on NP-complete
problems solving. June 2003. Amiens. France.
- [7]
- H. Batnini. Introduction of Redundant Constraints for Solving Systems of Distance Equations
Journal of the university of Saärbrück Sept, 2002. CALCULEMUS Autumn School 2002 in Pisa.
Participations (Talks) :
- JFPC 2005. 1ères Journées Francophones de Programmation par Contraintes.
Lens. Juin 2005. Session technique.
http://www.cril.univ-artois.fr/JFPC05
- JNPC 2004. 10e Journées Nationales pour la résolution de Problèmes NP-complets.
Angers. Juin 2004. Session commune JNPC/JFPLC.
http://www.info.univ-angers.fr/jnpc2004
- CP 2003. 9th International Conference on Principles and Practice of Constraint Programming.
Kinsale, County Cork, Ireland. Septembre 2003. Doctoral Programme.
http://www.cs.ucc.ie/cp2003
- JNPC 2003. 9e Journées Nationales pour la résolution de Problèmes NP-complets.
Amiens. Juin 2003. Session technique.
http://www.laria.u-picardie.fr/JNPC2003/
- EJC 2003 du GdR ALP.
Marne-la-vallée. Avril 2003. Exposés des jeunes chercheurs.
http://www-igm.univ-mlv.fr/ ejc2003
- CALCULEMUS Autumn School. Pise. Septembre 2002. Student poster session.
http://www.eurice.de/calculemus/autumn-school/getting_started.html



Next: About this document ...
Heikel Batnini
2005-08-01