On a :
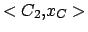 :
:
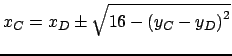 .
.
Projection des domaines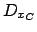 =
=
![$ D_{x_C} \cap ( D_{x_D} + \sqrt{[16,16] - {(D_{y_C} - D_{y_D})}^2}$](img360.png)
![$ D_{x_C}=[6,10] \cap ( [-3,3] + \sqrt{[16,16] - {( [-2,2] - [-3,3] )}^2})$](img361.png)
![$ D_{x_C}=[6,10] \cap ( [-3,3] + \sqrt{[16,16] - {[-5,5]}^2})$](img362.png)
![$ D_{x_C}=[6,10] \cap ( [-3,3] + \sqrt{[16,16] - [0,25]})$](img363.png)
![$ D_{x_C}=[6,10] \cap ( [-3,3] + \sqrt{[-9,16]})$](img364.png)
![$ D_{x_C}=[6,10] \cap ( [-3,3] + [-4,4] )$](img365.png)
![$ D_{x_C}=[6,10] \cap [-7,7]$](img366.png)
![$ D_{x_C}=[6,7]$](img367.png)
donc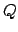 ={
={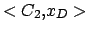 ,
, 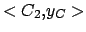 ,
, 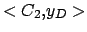 ,
, 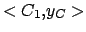 ,
, 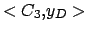 ,
,
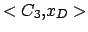 ,
, 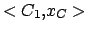 }.
}.
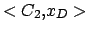 :
:
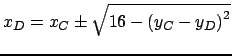 .
.
Projection des domaines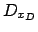 =
=
![$ D_{x_D} \cap ( D_{x_C} + \sqrt{[16,16] - {(D_{y_C} - D_{y_D})}^2}$](img370.png)
![$ D_{x_D}=[-3,3] \cap ( [6,7] + \sqrt{[16,16] - {( [-2,2] - [-3,3] )}^2})$](img371.png)
![$ D_{x_D}=[-3,3] \cap [2,11]$](img372.png)
![$ D_{x_D}=[2,3]$](img373.png)
donc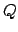 ={
={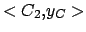 ,
, 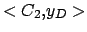 ,
, 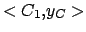 ,
, 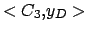 ,
,
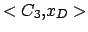 ,
, 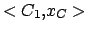 ,
, 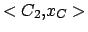 }.
}.
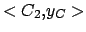 :
:
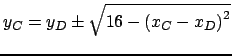 .
.
Projection des domaines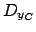 =
=
![$ D_{y_C} \cap ( D_{y_D} + \sqrt{[16,16] - {(D_{x_C} - D_{x_D})}^2}$](img376.png)
![$ D_{y_C}=[-2,2] \cap ( [-3,3] + \sqrt{[16,16] - {( [6,7] - [2,3] )}^2})$](img377.png)
![$ D_{y_C}=[-2,2] \cap [-3-\sqrt{7},3+\sqrt{7}]$](img378.png)
![$ D_{y_C}=[-2,2]$](img26.png)
donc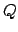 = {
= {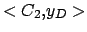 ,
, 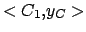 ,
, 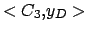 ,
,
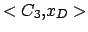 ,
, 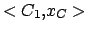 ,
, 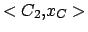 }.
}.
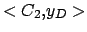 :
:
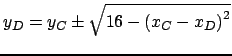 .
.
Projection des domaines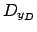 =
=
![$ D_{y_D} \cap ( D_{y_C} + \sqrt{[16,16] - {(D_{x_C} - D_{x_D})}^2}$](img381.png)
![$ D_{y_D}=[-3,3] \cap ( [-2,2] + \sqrt{[16,16] - {( [6,7] - [2,3] )}^2})$](img382.png)
![$ D_{y_D}=[-3,3] \cap [-2-\sqrt{7},2+\sqrt{7}]$](img383.png)
![$ D_{y_D}=[-3,3]$](img28.png) donc
donc 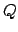 = {
= { 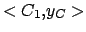 ,
, 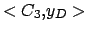 ,
,
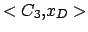 ,
, 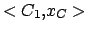 ,
, 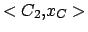 }.
}.
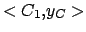 :
:
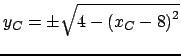 .
.
Projection des domaines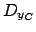 =
=
![$ D_{y_C} \cap ( \sqrt{[4,4] - {(D_{x_C} - [8,8])}^2} )$](img385.png)
![$ D_{y_D} = [-2,2] \cap ( \sqrt{ [4,4] - {([6,7]-[8,8])}^2} )$](img386.png)
![$ D_{y_D} = [-2,2] \cap [-\sqrt{3},\sqrt{3}]$](img387.png)
![$ D_{y_D} = [-\sqrt{3},\sqrt{3}]$](img388.png)
donc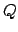 = {
= { 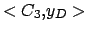 ,
, 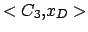 ,
, 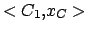 ,
, 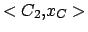 ,
, 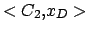 ,
, 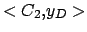 }.
}.
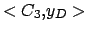 :
:
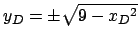 .
.
Projection des domaines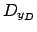 =
=
![$ D_{y_D} \cap ( \sqrt{[9,9] - {D_{x_D}}^2} )$](img390.png)
![$ D_{y_C} = [-3,3] \cap ( \sqrt{ [9,9] - [2,3]^2 } )$](img391.png)
![$ D_{y_C} = [-3,3] \cap [-\sqrt{5},\sqrt{5}]$](img392.png)
![$ D_{y_C} = [-\sqrt{5},\sqrt{5}]$](img393.png) donc
donc 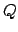 = {
= { 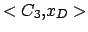 ,
, 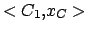 ,
, 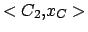 ,
, 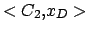 ,
, 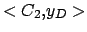 ,
, 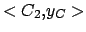 }.
}.