 |
 |
 |
 |
The powerful level-of-detail of the point sets can also be used for dynamic objects. For the following objects, we simulated movement of the trees in a turbulent breeze, by moving the single points according to the local wind and the point's distance to the stem. We still obtain 20 frames per second.

There is also a video clip showing the point rendered forest: 
This simple example shows the power of point representations: Visually complex objects can be rendered and modified interactively, with only little precomputation and memory requirements. By adapting the point number (and the point size accordingly), frame rate constraints can easily be met. Such frame rate constraints are paramount for all kinds of virtual reality and game-like applications, where a decrease in image quality is more acceptable than a frame rate degradation.
The advantages for rendering also apply to many other problems related to interactive applications and computer games, like dynamics computations, collision detection, visibility determination etc., where the required accuracy mainly depends on the distance to the user(s). Furthermore, as we will show in the following, points are very efficient with procedural models. All changes to a virtual world that cannot be precomputed because they happen due to user input (impacts or bullet holes on a wall, deformed objects, interactively modelled objects, ripples in a lake created by the user, see application scenario section), are usually described procedurally, with user interactions as parameters. Transforming this procedural description to an appropriate polygonal representation, e.g. for rendering, can be difficult. We believe that points are often a better means in these cases.
Of course points are not always the best solution. Big rectangles should remain rectangles and it will take a long time before home computers are fast enough so that all image textures can be replaced by "real" texture geometry. However, points are obviously a good means whenever triangles become smaller than a pixel. It does not really make sense to render triangles of subpixel size, and in particular not at 50 Hz.
In this context the analogy to ray tracing is interesting: even an oversampling
ray tracer can only sample a few triangles per pixel. That's why for very
complex scenes ray tracing becomes faster than scanline rendering. It is
very fast to ray trace a scene with 100,000,000 triangles if 99,999,990
of them are within a single pixel, whereas each scan-line renderer will
spend all its time on this one particular pixel. For the remaining pixels,
however, scanline rendering will be ways faster. Point-based rendering
is in between. It uses sample sets with a density fitting to image resolution
like ray tracing, but it projects object points from world to image space
like scanline renderer, so it does not require the costly ray casting operations.
 |
 |
|

For the adaptive sample insertion described above, we use the sqrt5-sampling scheme. The principle of this scheme is explained in the figure below: On the left, we see a rectangle sampled by four points. In order to sample the neighborhood of each point, we generate samples at relative positions (2/5,1/5), (-1/5,2/5), (-2/5,-1/5), (1/5,-2/5) (center left). Note that the original four points plus the 16 new ones again form a regular grid. The new grid distance is 1/sqrt(5) of the original grid and the grid is rotated by about 26 degrees. We can apply the same refinement rule to the new grid to further increase the resolution (center right). In practice, the refinement will be local, i.e. only for critical points new nearby points are generated, resulting in an adaptive, deterministic sampling pattern (right)
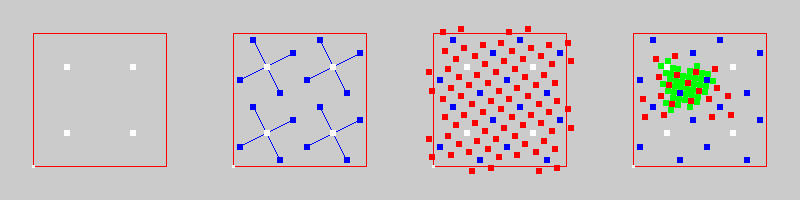
You can download a video clip showing the ideas of sqrt(5) sampling: 
 |
 |
 |
Procedural modifiers: displaced sphere, "holy" sphere, wickerwork basket. Note the topology changes form the original sphere (center) and the truncated cone (right).
As discussed above, procedural object descriptions are essential for all applications that allow user interaction. One can think of many examples, from users modelling objects in a virtual reality environment to players shooting holes into walls.
The sqrt(5) video clip also shows procedural modifiers: 
 |
 |
A videoclip shows the terrain rendering: 
 |
 |
We apply a purely heurisitc lighting model to the clouds by computing a virtual shading normal that is in opposite direction to the density gradient, which can be computed cheaply from our cloud model. Although this model has no physical basis, the increase in realism is enormous. The cloud in the right image above is rendered by 65.000 points only (consider that the latest off-the-shelf graphics cards can render 10,000,000 points per second).
We also have a video sequence about cloud rendering: 
 |
 |
Two snapshots of an interactive session in a dynamic procedural virtual world. The user navigates at about 8 fps. The trees are moving in the wind and the user ``throws rocks'' into the lakes. The terrain is precomputed and stored in a texture.
 |
 |
Interactive design of an interior environment. To a radiosity solution of an office rendered with polygons, we added a complex tree, a wicker work basket and a paper weight, all displayed with 75,000 points. After turning on the fan, the tree is moving in the wind (center, 13 fps at 400x400). The images on the right show the interactive change of parameters of procedural objects. Top row: changes at 4 fps, bottom row: 8 fps, the last one at 1.5 fps.

 |
 |
 |
Interactive design of an outdoors scene (resolution 400x400). We start with a simple terrain (left: 23,000 points, 6 fps), add 1000 chestnut trees made of 150,000 triangles each and add two clouds (280,000 points, 5 fps). If we increase accuracy, we get the right image using 3,300,000 points after 2 sec.