Etienne Bertin, Jean-Michel Billiot, Rémy Drouilhet

k-Nearest-Neighbours Gibbs Point Processes

Dans cet exposé, nous étudions les processus ponctuels spatiaux de Gibbs dont les interactions de paires sont gérées par le graphe des k-plus-proches voisins. Ces interactions sont associées à un potentiel de paires permettant à toute configuration finie $\varphi$ de points d'être gérée énergétiquement de la manière suivante :

$$V\left( \varphi \right) =\sum\limits_{i=1}^k\sum\limits_{x\in \varphi }g_i\left( d_i\left( x,\varphi \right) \right)$$

où $d_i\left( x,\varphi \right)$ représente la distance de x au $i^{\grave{e}me}$ plus proche voisin de x dans $\varphi$ ( $\char93 \varphi \geq k$) et les fonctions g_i sont majorées par une fonction $\widetilde{g}$ positive bornée, décroissante qui tend vers 0 à l'infini. L'originalité de notre modèle est que les relations de voisinage dépendent de la réalisation du processus comme pour le cas d'autres processus spatiaux de Gibbs introduits par Baddeley et Møller [BM89].

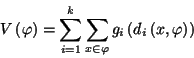
Nous montrerons l'existence d'états de Gibbs pour le modèle des k-plus-proches voisins dans $\hbox{I\kern-.2em\hbox{R}}^d$en s'inspirant notamment des travaux de Preston [Pre76] (les états de Gibbs sont solutions des équations d'équilibre ou équations de Dobrushin-Lanford-Ruelle [Rue69,Rue70]). Notre résultat est basé sur la notion de quasilocalité et sur le fait que l'énergie nécessaire à l'insertion d'un point x dans une configuration $\varphi$ est minorée : $E\left( x ,\varphi \right) = V\left(\varphi \cup \{x\} \right) - V\left(\varphi \right) \geq -K$où K est une constante positive. On peut montrer que

$$E\left( x ,\varphi \right) = \sum\limits_{i=1}^k\left( g_i\l... ... -g_i\left( d_i\left( y,\varphi \right) \right) \right) \right)$$

et que la minoration de $E(x,\varphi)$ est reliée au problème géométrique de Tammes qui consiste à placer N points sur l'hypersphère S^d-1 en maximisant le minimum des angles [Ber92] :

$$\gamma _N^d=\max\limits_{\varphi \subset S^{d-1} \atop \char9... ...in\limits_{z_i,z_j\in \varphi }\gamma \left( z_i,0,z_j\right).$$

où $\gamma \left( z_i,0,z_j\right)$ est l'angle au centre du triangle $\overline{z_i0z_j}$.

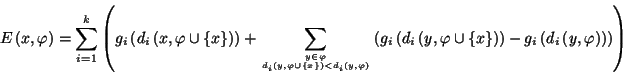
Finallement, on donne des résultats de simulation basés sur un algorithme de naissances et morts utilisant la dynamique de Metropolis-Hasting [GM94]. Pour l'insertion (naissance) d'un point x dans une configuration et la suppression (mort) de x d'une configuration, on utilise le graphe de Delaunay (le $i^{\grave{e}me}$ plus proche voisin de xest à une distance inférieure ou égale à i au sens du graphe de Delaunay de la configuration contenant le point x) [BBD99].