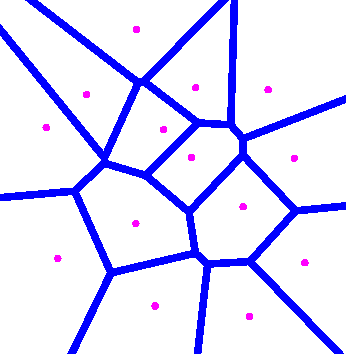
Definition : The Delaunay triangulation of S is the geometric dual of the Voronoi diagram of S : two sites of S are linked by an edge in the Delaunay triangulation if and only if their cells are incident in the Voronoi diagram of S.
 |
Definition :
Let S a set of n sites in Euclidean space of
dimension d. For each
site p of S, the Voronoi cell V(p) of p is
the set of points that are closer to p than to other
sites of S.
The Voronoi diagram V(S) is the space partition
induced by Voronoi cells. Definition : The Delaunay triangulation of S is the geometric dual of the Voronoi diagram of S : two sites of S are linked by an edge in the Delaunay triangulation if and only if their cells are incident in the Voronoi diagram of S. |
| Voronoi diagrams are very useful structures, they represent distance relationships and growth phenomena. Thus, it is not surprising to use Voronoi diagrams to modelize crystals growth or the big objects of the universe, and to observe them in natural objects such as carapace turtle or neck of giraffe. Voronoi diagrams are also data structures solving many problems such as nearest neighbor search or motion planning. Study of Voronoi diagrams, their mathematical properties, their computation and their generalizations was and still is a main subject in computational geometry. Prisme project contributions deals with combinatorial and algorithmic aspects, extension to non Euclidean metrics and applications in shape reconstruction. | 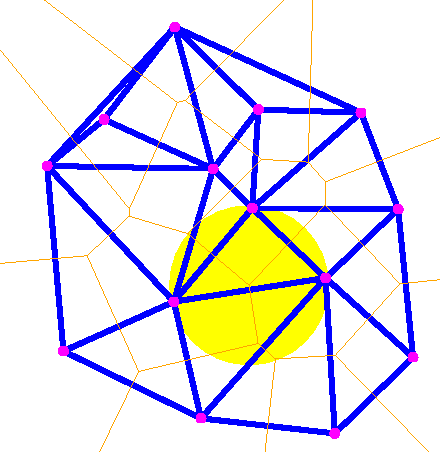 |
| Last modified: Fri Jan 7 08:51:30 MET 2000 | Olivier Devillers | Topics |
|