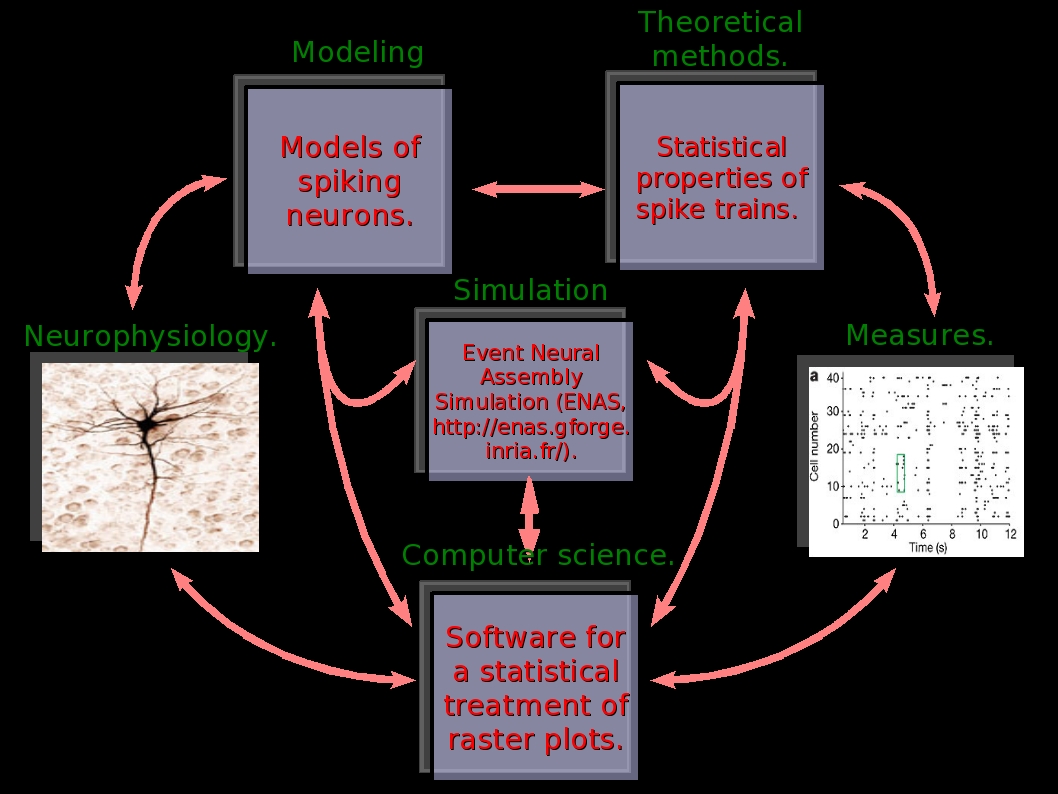
Information transport by neurons is mediated by spikes trains. How information is encoded remains an open issue despite numerous significant experiments and theoretical advances. Thus, the analysis of spike trains obtained from in vivo or in vitro experimental data, requires suitable statistical models, while the models commonly used are ad hoc (e.g. Poissonnian) and are not necessarily the most adapted. Recent advances have attempted to construct these models from general principles. A significant example is due to Schneidman and collaborators [Schneidman-etal, 06]. In experiments on Salamander retina, these authors have shown that spike trains statistics is well described by a probability distribution of Gibbs type, obtained via a variational principle, where one maximizes statistical entropy with the contraints of matching experimental measures of spikes correlations. We believe that there is, in this approach, a fundamental method that can be formalised and developed in the framework of dynamical systems theory and statistical physics. With this idea in mind, we are developing the following research directions. 

On the one hand we are analysing models of spiking neural networks using tools from dynamical systems theory and ergodic theory (especially thermodynamic formalism). We have firstly made a complete characterization of the dynamics exhibited by Integrate and Fire models (with conductance based synapses) and we have especially shown how spike trains provide a symbolic coding for dynamics [Cessac:07,Cessac-Vieville:08]. Since these models are considered as rather good approximations of real neurons (see for example [Jolivet-etal:06], and our recent paper [Rostro-etal:09] ) we expect that this analysis provide relevant issues in theoretical and experimental neuroscience.  Our main goal is the characterization of spikes train statistics generated by these models dynamics. We have recently shown how the thermodynamic formalism used in ergodic theory allows the construction of Gibbs distribution on spike trains via a variational principle, especially after synaptic adaptation mechanisms (synaptic plasticity) [Cessac-etal:09]. In particular, a general class of synaptic plasticity rules can be formulated in terms of the variation of a quantity, the topological pressure, closely related to thermodynamic potentials in statistical physics. As a consequence of this analysis spike trains statistics are more likely described by Gibbs probability distributions than by the classical Poisson distributions. The other way round, we believe that some variational problems could be solved by spiking neural networks after a suitable training. We are also investigating this issue. See section “Theoretical developments”.

On the other hand, we are developing numerical tools for the analysis of spike trains, such as entropy estimation, Kullback-Leibler divergence and approximation of probability distributions of spike trains from raster plots. Part of these numerical tools has been integrated in the ENas (Event Neural Assemby Simulation) library developed at INRIA. Plugins and demos are available in this web site. Especially we are able to approximate the empirical measure associated to a realisation of a spike train, by a Gibbs measure with a suitable (finite range) potential, estimated by experimental constraints. See section “Numerical developments.”

We want to use these tools, combined with the information obtained from the theoretical analysis, to study experimental data. Especially, we are working on data obtained at Institut de Neurosciences de la Mediterrannée (INCM) on the monkey in collaboration with the DyVa team at INCM and F. Grammont (Nice University). We are also working in collaboration with A. Palacios, Centro de Neurociencia in Valparaiso on the characterization of non standard ganglion cells in the retina. The potential outcome are twolfold. On a fundamental ground, the goal is to make a step further in a promising research area: the statistical characterization of spike trains obtained from in vivo and in vitro data. On a practical ground, the goal would be, on the long term, to provide a software allowing an automatic treatment of experimental data. See section “Applications.”