Mesoscopic modeling of cortical columns, bifurcations, and imaging
|
Mesoscopic modeling of cortical columns, bifurcations, and imaging |
|
|
|
|
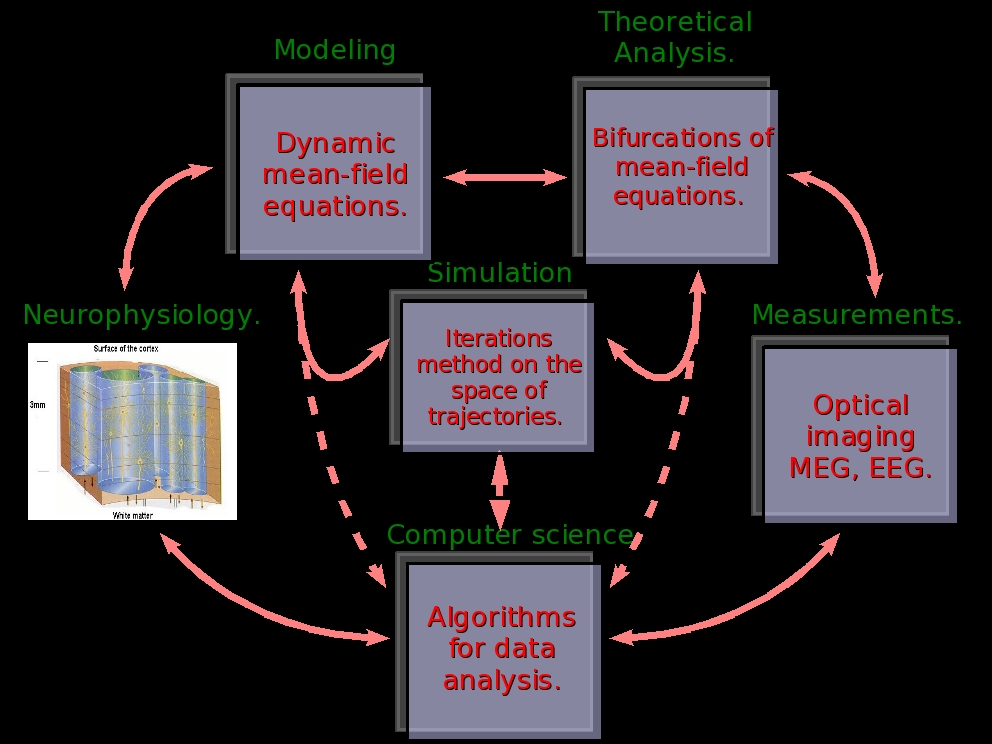
Brain Imaging techniques such as Optical Imaging or MEG-EEG require a precise modeling of the cortex electrical activity at space scales smaller than 1 mm2 of cortical matter. It is therefore useful to propose models of this activity, than can be analysed mathematically. In this spirit cortical columns models have been proposed by several authors [Lopes-et-al, 1976], [Jansen-Rit, 1995]. To model cortical activity at larger scales it is then necessary to consider spatially extended models, like neural masses models [Folias-et-al:05, Coombes:05, Blomquist:05]. The mathematical properties of these models can then be analysed using bifurcations techniques [Ermentrout-Cowan:79a,b, Bressloff-et-al:01a,01b,03, Grimbert-Faugeras; 06].
However, these models are not obtained from the dynamics at a "microscopic" scale (neurons), but instead via a phenomenological approach describing directly the local field at a mesoscopic scale. Thus, in most approaches, equations are obtained by a description of neural population i in terms of an average potential Vi and an average frequency rate ni. Moreover, one postulates a relation ni = Si (Vi) (where Si is a sigmoidal function) which holds for neurons (microscopic scale). Therefore, one applies at the mesoscopic scale a relation only valid at a microscopic scale. This relies on questionable assumptions, neglecting for example the local fields fluctuations, which may have an important impact on dynamics. As a matter of fact, a natural question is how to generate the phenomenological equations for the mesoscopic dynamics of cortical columns via microscopic dynamics. Methods from statistical physics allows to do this and to make an analysis of these equations.
In this spirit we are developing dynamic mean-field methods to characterize neural networks models describing the activity of P neuronal populations in cortical columns, including non stationary dynamics and field fluctuations (see section "Modeling cortical columns dynamics"). A primary goal is then to be able to characterize mathematically or numerically the dynamical regimes exhibited by a realistic model of a cortical column model, with several neural populations, and with a connectivity scheme based on anatomic data [Thomson-Lamy, 07]. This study is the first step toward the characterization of local field potentials at a scale corresponding precisely to the resolution of optical imaging or MEG. Taking into account the fluctuations and correlations of local field should bring, as we checked on simple examples, a richer phenomenology. This requires a detailed analysis of the model dynamics. This last point is addressed by a bifurcation analysis of mean-field equations. Especially, techniques analysing the effects of symmetries and symmetries breaking are currently under investigations. Indeed, because of the regular disposition of cortical columns, a mathematically fruitful simplification assumes invariance properties such permutations between neurons or groups of neurons. This allows to give to the model a structure simplifying its analysis (see section "Bifurcation analysis of cortical columns dynamics.").
In parallel with this mathematical analysis we have developed a new numerical method where one iterates a map acting on bounded times trajectories of the law of the mean field process. This method allows to access non stationary regimes corresponding for example to having time dependent inputs.
The ultimate goal is to compare the dynamical behaviour predicted by our analysis to real experimental data to better understand the link between what is measured and the underlying cortical activity. Thus, to validate part of our theoretical and numerical results, we want to compare them to the cortical activity of the visual system (V1/V2) measured with MEG and intrinsic optical imaging. The MEG is done in collaboration with M. Clerc et T. Papadopoulo (ODYSSEE). The optical imaging part is done in collaboration with DyVa team in INCM, as a continuation of F. Chavanne (INCM) and F. Grimbert (ODYSSEE) work [Grimbert-et-al, 07, Grimbert-Chavanne, 07] (see section "Measuring cortical columns dynamics.").
Bibliography.
[Blomquist-et-col, 05] . Blomquist, J. Wyller, and G. Einevoll. Localized activity patterns in two-population neuronal networks. D, 206:180–212, (2005).
[Bressloff-Cowan:03] Bressloff P.C., Cowan J.D., “The functional geometry of local and horizontal connections in a model of V1”, Journal of physiology, vol. 97, N° 2-3, 221-236 (2003).
[Bressloff-et-al:01a] Bressloff P.C., Cowan J.D., Golubitsky M., Thomas P.J., Wiener M.C., “Geometric visual hallucinations, Euclidean symmetry, and the functional architecture of striate cortex”, Philos. Trans. R. Soc. London B, Biol. Schi. 356 (1407): 299-333 (2001).
[Bressloff-et-al:01b] Bressloff P.C., Cowan J.D., Golubitsky M., Thomas P.J., “Scalar and pseudoscalar bifurcations with application to pattern formations on the visual cortex”, NonLInearity, Vol. 14, Num 4, 739-775 (2001).
[Ermentrout-Cowan:79a] Ermentrout G.B., Cowan J.D., “A mathematical theory of visual hallucinations patterns”, Biological Cybernetics, 34, 137-150, (1979)
[Ermentrout-Cowan:79b] Ermentrout G.B., Cowan J.D., “Temporal oscillations in neuronal nets. ”, J Math Biol. 1979 Apr 18;7(3):265-80.
[Folias-et-al,05] Folias, S. E., Bressloff, and C. Paul. Breathing pulses in an excitatory neural network. SIAM Journal of Applied Dynamical Systems, 3(3):378–407, 2004.
[Grimbert-Faugeras:06] F. Grimbert and O. Faugeras. Bifurcation analysis of Jansen’s neural mass model. Neural Computation, 18(12):3052–3068, December 2006.
[Grimbert-Chavane,07], F. Grimbert, F. Chavane, F., Neural Field Model of VSD Optical Imaging Signals, rapport de recherche INRIA, N° 6398, 2007. https://hal.inria.fr/inria-00199917
[Grimbert-et-al, 07], F. Grimbert, O. Faugeras, F. Chavane, From neural fields to {VSD} optical imaging, CNS 2007.
[Jansen-Rit, 1995] B. H. Jansen and V. G. Rit. Electroencephalogram and visual evoked potential generation in a mathematical model of coupled cortical columns. Biol. Cybern., 73:357–366, 1995.
[Lopes-et-al, 1976] F. Lopes da Silva, A. van Rotterdam, P. Barts, E. van Heusden, and W. Burr. Model of neuronal populations. the basic mechanism of rhythmicity. M.A. Corner, D.F. Swaab (eds) Progress in brain research, Elsevier, Amsterdam, 45:281–308, 1976.
[Thomson-Lamy, 07] . Thomson and C. Lamy. Functional maps of neocortical local circuitry. in neuro- science, 1(1):19–42, 2007.