|
My name is Viet-Dung Doan - PhD Student ,
INRIA Sophia Antipolis
2004 Route des Lucioles, BP93, 06902, France
|
|
|
My name is Viet-Dung Doan - PhD Student ,
INRIA Sophia Antipolis
2004 Route des Lucioles, BP93, 06902, France
|
|
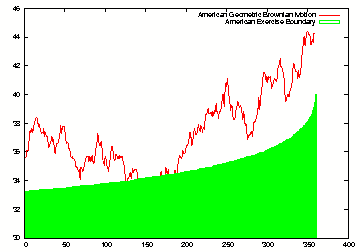 Geometric Brownian Motion with exercise boundary
Geometric Brownian Motion with exercise boundary
|
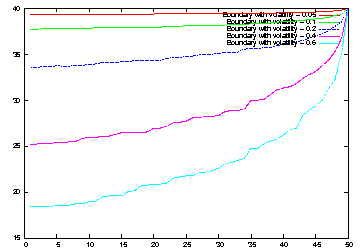 Frontier exericise with stochastic volatilities
Frontier exericise with stochastic volatilities
|
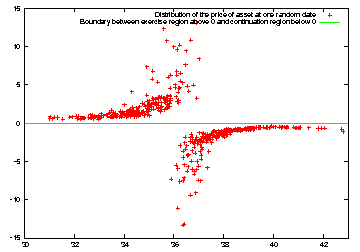 Exercise region above 0 and continuation region below 0 at a random date
Exercise region above 0 and continuation region below 0 at a random date
|
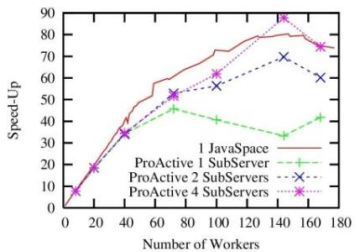 Performance
Performance
|
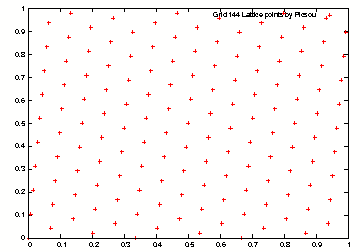 Grid 144 lattice points generated in Java
Grid 144 lattice points generated in Java
|
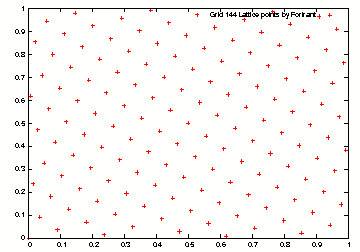 in Fortrant in Fortrant
|
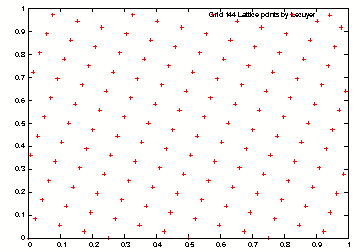 by L'ecuyer by L'ecuyer
|
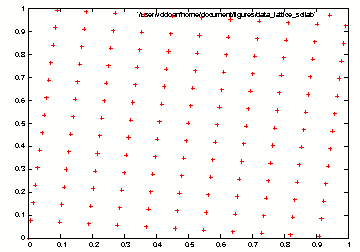 in Scilab in Scilab
|
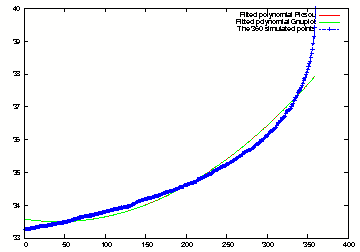 Least Square Regression 2th order polynomial
Least Square Regression 2th order polynomial
|
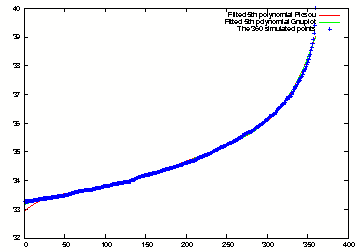 Least Square Regression 5th order polynomial
Least Square Regression 5th order polynomial
|
 Weighted and normal least square regression
Weighted and normal least square regression
|
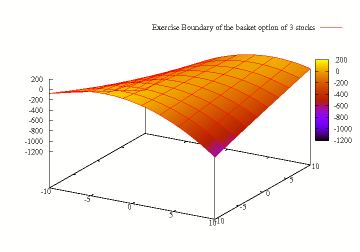 Exercise boundary of American Basket Option (3 stocks)
Exercise boundary of American Basket Option (3 stocks)
|