Deug MASS 2 Année 2000/2001
U.N.S.A.



ALGORITHMIQUE ET STRUCTURES DE DONNEES

TP 9

Récursivité (suite)

1. Division par deux

On souhaite écrire un méthode calculant la division par 2 d'un entier, mais sans utiliser l'opérateur / de Java, seulement les opérateurs + et -.

Pour cela on remarque la propriété suivante :

$$\frac{m}{2} = (1 + \frac{(m-2)}{2}) \mbox{ si } m > 1$$

Ajouter dans la classe Recursivite une méthode récursive public static int division2Rec(int m) qui retourne la division par 2 de l'entier m.

2. Multiplication d'entiers

On souhaite écrire un méthode calculant le produit de deux entiers, mais sans utiliser l'opérateur * de Java, seulement les opérateurs + et -.

Pour cela on remarque la propriété suivante :

$$m \times n = (m + (n-1) \times m) \mbox{ si } n > 0$$

Ajouter dans la classe Recursivite une méthode récursive public static int multiplicationRec(int m, int n) qui retourne le produit des entiers m et n.

3. Coefficients binômiaux

Ajouter dans la classe Recursivite une méthode récursive public static int binomial(int n, int p) qui retourne C_n^p, le nombre de combinaisons de p éléments d'un ensemble comportant n éléments.

Une définition récursive de C_n^p est donnée par :

$$\left\{ \begin{array}{ll} C_{n}^{p} = 0 & \mbox{ si } \; n < ... ... si } \; p = 0 \; \mbox{ ou } \; n = p \, \end{array} \right.$$

pour les cas de base et par :

C_n^p = C_n-1^p-1 + C_n-1^p

pour le cas de récurrence.

4. Recherche dichotomique

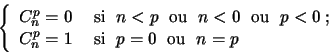
La recherche dichotomique est un moyen de trouver rapidement une valeur dans un tableau trié. Elle repose sur le principe du « diviser pour régner ».

L'idée est simple et consiste à choisir un indice particulier kcorrespondant à la moitié du tableau trié t. Trois cas se présentent :

• l'élément recherché se trouve à cet indice;
• l'élément recherché est plus petit que l'élément t[k], dans ce cas, on continue la recherche par le même procédé dans la partie gauche du tableau;
• l'élément recherché est plus grand que l'élément t[k], dans ce cas, on continue la recherche par le même procédé dans la partie droite du tableau

Ecrire alors dans la classe Recursivite une méthode récursive public static int rechercheDicho(Tableau t, int g, int d, int e) qui prend en argument :

• t, un tableau trié;
• g, la borne gauche du tableau à partir de laquelle effectuer la recherche;
• d, la borne droite du tableau jusqu`où effectuer la recherche;
• e, la valeur de l'élément à rechercher.

Elle retourne l'indice dans le tableau de l'élément recherché et -1 s'il n'est pas trouvé.

À chaque appel récursif, la méthode vérifie si les indices g et dsont corrects, calcule l'indice médian entre i et j et effectue à partir de cet indice médian k le traitement décrit précédemment.

5. Les tours de Hanoï

Le but de cet exercice est de résoudre le problème des tours de Hanoï en utilisant un algorithme récursif. Rappelons d'abord le principe de ce jeu.

N disques de diamètres deux à deux différents sont initialement enfilés sur une « tige de gauche ». Ils sont disposés de telle sorte que leurs diamètres décroissent de la base de la tige vers le sommet de la tige (voir figure 1). Le but du jeu est de déplacer ces N disques vers une « tige de droite » en se servant d'une « tige du milieu », et en respectant les règles suivantes :

1.

seul un disque peut être déplacé à la fois ;

2.

un disque ne doit jamais être placé sur un disque de diamètre plus petit ;

3.

chaque disque doit à tout moment se trouver sur une tige.

La solution de ce problème peut s'écrire très simplement sous forme récursive. En effet, on peut en proposer la solution suivante :

1.

déplacer les N - 1 disques du haut de la tige de gauche vers la tige du milieu en utilisant la tige de droite comme tige intermédiaire ;

2.

déplacer le dernier disque de la tige de gauche vers la tige de droite ;

3.

déplacer les N - 1 disques de la tige du milieu vers la tige de droite en utilisant la tige de gauche comme tige intermédiaire.

Avant de programmer cet algorithme, testez son fonctionnement sur papier en faisant son arbre d'appel pour N = 3.

Ajouter alors dans la classe Recursivite une méthode déplacerTour, qui prend en argument un entier N représentant le nombre disques à déplacer, et trois arguments de type caractère (char), src, inter et dest. Cette méthode résout le problème des tours de Hanoï pour le nombre N de disques spécifié et affiche l'action effectuée lors de chaque déplacement.

Par exemple, le résultat de déplacerTour(2, 'A', 'B', 'C') sera l'affichage de :

Disque 1 de A vers B
Disque 2 de A vers C
Disque 1 de B vers C

  

Figure: Tours de Hanoï. Les disques sont numérotés de 1 à N(ici, N = 5), du plus petit au plus grand.