Some works

Hybrid meshes partitions
I worked on different strategies to reduce the load balancing when dealing with highly complicated configuration (local refinement, hybrid meshes, local observables, ...).

MHM Mesh generator (3D)
Development of a MHM Mesh generator for complex configuration by exploiting CAD features from GMSH 3.0+. This is the first step for the implementation of the 3D MHM-DGTD solver.
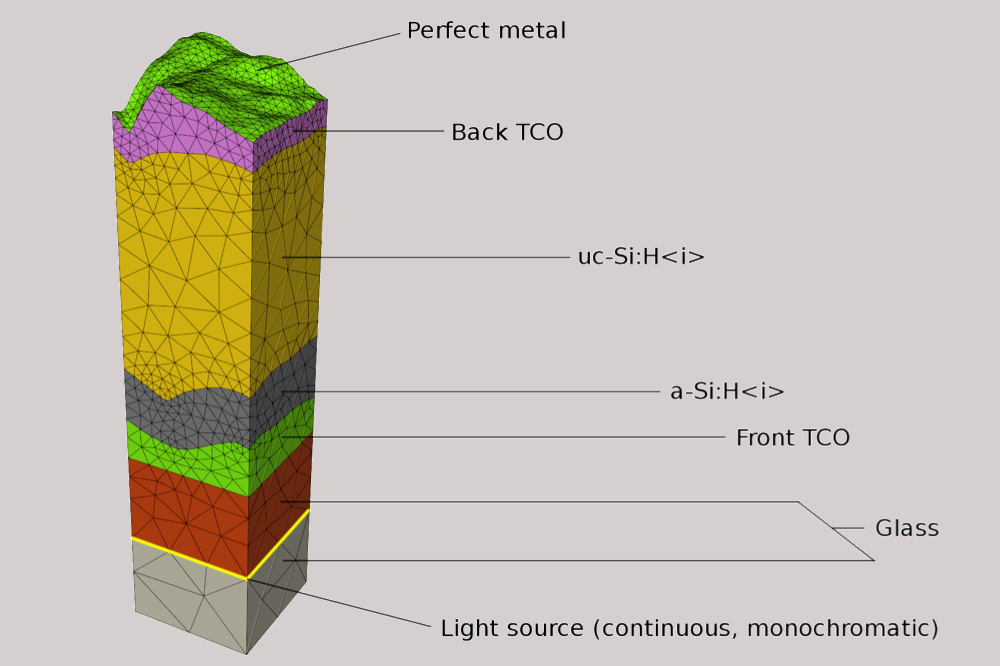
Simulation of light trapping in thin-film solar cells
We study light trapping in a silicon-based thin-film solar cell setup that consists of several randomly textured layers using DGTD solver DIOGENeS5+. The focus is on a-Si:H5 and µc-Si:H5* which belong to the family of disordered semiconductors. More information about this case on Nachos highlights of the month.
5. Amorphous silicon
5*. Microcrystalline silicon
5+. DIscOntinuous GalErkin Nanoscale Solvers
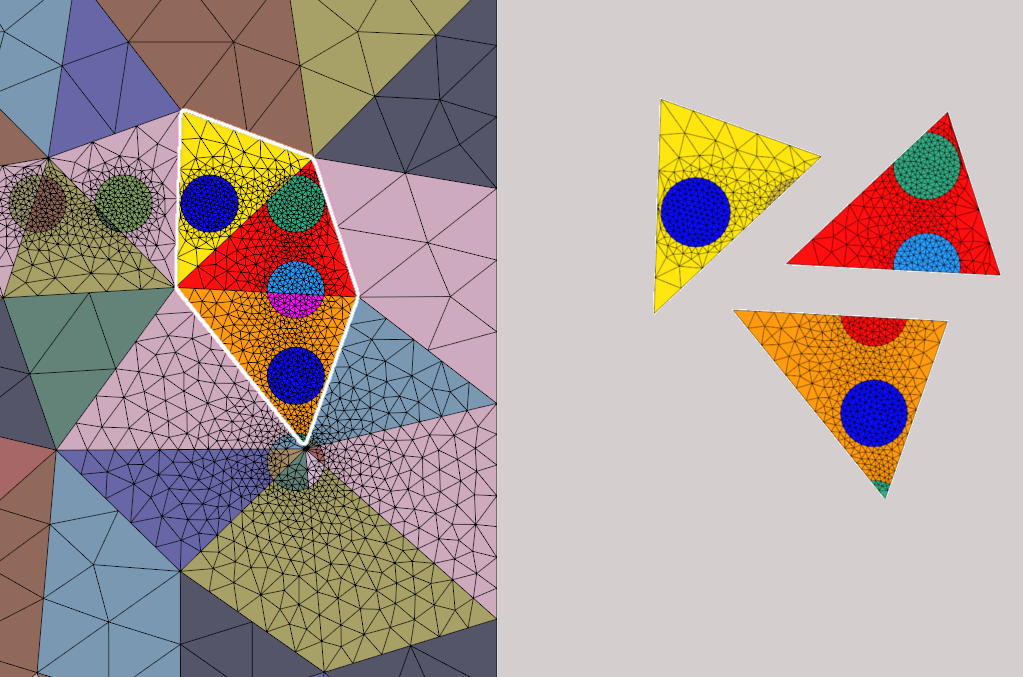
MHM-DGTD for Maxwell's Equations
Work on the MHM-DGTD4 code of Raphaël Léger for the 2D time domain Maxwell's equations. Developpement of a tool for the generation of the coarse and of the local meshes of complex configuration. Implementation of local order per edges to deal with heterogeneous media.
4. Multiscale Hybrid-mixed Method + Discontinuous Galerkin Time domain on the local problem

DGTD on hybrid meshes for textured layers type domain

Near perfect solar absorption in ultra-thin-film GaAs photonic crystal
Here we are interested by solar absorption in ultra-thin-film GaAs3 photonic crystals. GaAs solar cells offer an alternative material to mostly used silicon-based solar cells.
3. Gallium arsenide
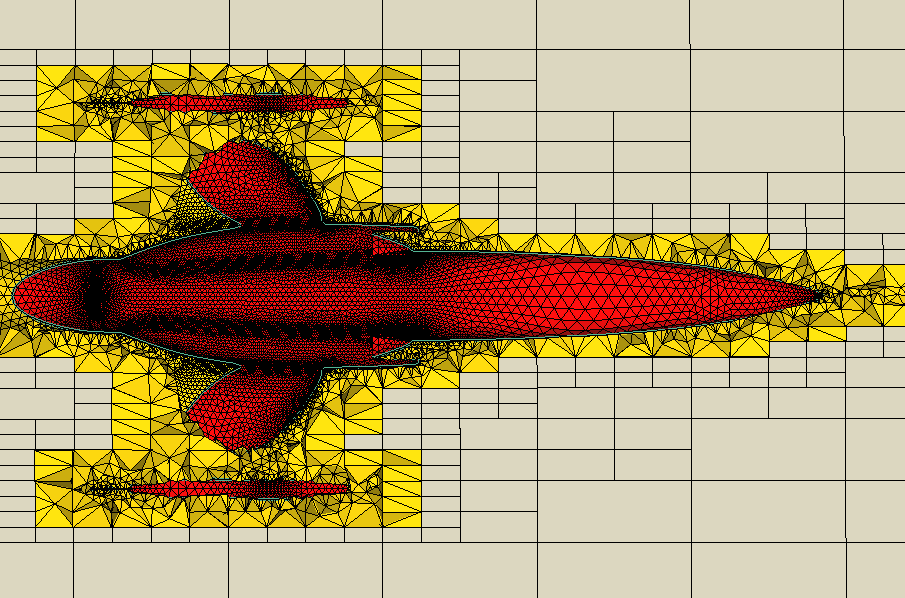
Hybrid mesh generator
Developement from scratch of THYMuS2, a non conformal hybrid mesh generator of complex geometries in the context of ANR TECSER project.
2. Toolbox for Hybrid Mesh

HDGM frequency domain
Worked on the HORSE1 platform of Ludovic Moya , platform based on HDG1* method for solving the time-harmonic Maxwell’s equation in 3D and add into it the possibility to use tetrahedral/hexahedral hybrid meshes.
1. High Order solver for Radar cross Section Evaluation
1*. Hybrid Discontinuous Galerkin Methods