Vous pouvez télécharger une version postscript compressée de ma thèse !
Vous pouvez télécharger une version postscript compressée de ma thèse !
Thèse de Doctorat de l'Ecole Polytechnique, Mathématiques Appliquées, 1999RésuméLa thèse comporte une partie théorique sur la stabilité des systèmes dynamiques à événements discrets, et une partie plus appliquée sur le contrôle de flux dans les réseaux de télécommunication, qui a motivé la première et en utilise les techniques.
Dans la première partie, on s'intéresse tout d'abord à l'approche markovienne de la stabilité des systèmes dynamiques à événements discrets. On applique notamment la méthode dite des limites fluides à un réseau de files d'attente mixte, à la fois ouvert et fermé. On considère ensuite l'approche trajectorielle de la stabilité. Dans un premier temps, on présente la règle de saturation pour les systèmes monotones-homogènes et séparables, qui s'applique par exemple aux réseaux de files d'attente à une seule classe de clients. On démontre ensuite la règle de saturation en boucle fermée pour les systèmes monotones-invariants, qui s'applique à certains réseaux de files d'attente à plusieurs classes de clients. Ces résultats sont illustrés par de nombreux exemples.
La deuxième partie se consacre au contrôle de flux dans les réseaux de télécommunication. On présente tout d'abord les objectifs du contrôle de flux et les principaux mécanismes utilisés. On étudie ensuite les performances du contrôle de flux à fenêtre statique. On considère notamment l'influence des caractéristiques statistiques du trafic transverse sur l'efficacité du contrôle de flux. Enfin, on s'intéresse au contrôle de flux à fenêtre dynamique, utilisé par le protocole TCP dans l'Internet. On étudie l'allocation et l'utilisation des ressources du réseau réalisées par les versions Reno et Vegas de TCP.
Mots-clés
Systèmes à événements discrets, chaînes de Markov, théorie ergodique ;
Réseaux de télécommunication, contrôle de flux, Internet, TCP.
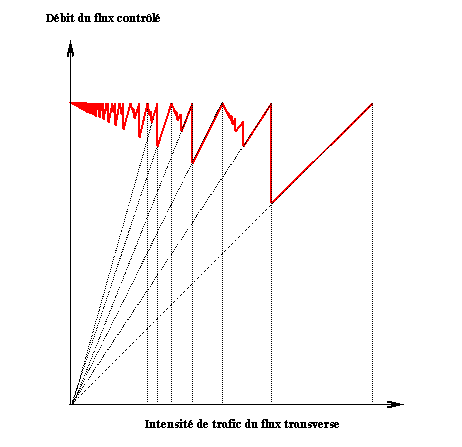
Comportement fractal du contrôle de flux à fenêtre
Page d'accueil