par Juliette Leblond, chargé de recherche à l'INRIA (projet Miaou), - et Mohamed Jaoua, professeur à l'ENIT (LAMSIN)1
Complétion de données dans les classes de Hardy et applications aux problèmes inverses
Pour fixer les idées, considérons le problème inverse suivant, dans
un domaine lisse ![]() de
de
![]() .
.
(PR) Etant donné un flux ![]() (
(
![]() ) ainsi que des
mesures
) ainsi que des
mesures ![]() sur un sous-ensemble
sur un sous-ensemble ![]() de la frontière
de la frontière
![]() ,
trouver un coefficient d'échange
,
trouver un coefficient d'échange ![]() tel que la solution
tel que la solution ![]() de :
de :
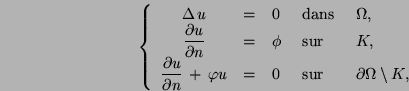
L'approche proposée consiste à exprimer les propriétés
d'harmonicité et de régularité de ![]() dans
dans
![]() en
termes d'analyticité et de bornitude d'une certaine fonction de la
variable complexe
en
termes d'analyticité et de bornitude d'une certaine fonction de la
variable complexe ![]() (on fait l'identification
(on fait l'identification
![]() ), donnée sur la partie
), donnée sur la partie ![]() de la
frontière accessible aux mesures par
de la
frontière accessible aux mesures par
![]() .
.
Si l'on désigne par
![]() l'espace de Hardy des
fonctions analytiques dans
l'espace de Hardy des
fonctions analytiques dans ![]() et bornées dans
et bornées dans
![]() , pour une mesure
, pour une mesure ![]() positive et
sous des hypothèses de régularité adaptées, (PR)
peut se formuler comme :
positive et
sous des hypothèses de régularité adaptées, (PR)
peut se formuler comme :
étant donnée des mesures sur
![]() d'une
fonction
d'une
fonction ![]() appartenant à
l'espace de Hardy
appartenant à
l'espace de Hardy
![]() , trouver l'extension
, trouver l'extension ![]() de
de ![]() à
à
![]() ,
,
ou plutôt, pour être robuste aux erreurs de mesure, sous forme d'un
problème extrémal borné (PEB) :
étant donnée des mesures sur
![]() d'une
fonction
d'une
fonction ![]() , trouver son
meilleur approximant
, trouver son
meilleur approximant ![]() dans
dans
![]() en norme
en norme ![]() ,
vérifiant une contrainte adaptée sur
,
vérifiant une contrainte adaptée sur
![]() .
.
Ceci s'avère
être une méthode originale et efficace pour aborder les propriétés de
stabilité ou développer des algorithmes de résolution pour
certains problèmes inverses. En particulier, la solution ![]() de (PR) s'exprime alors (et se calcule) en fonction de
de (PR) s'exprime alors (et se calcule) en fonction de ![]() sur
sur
![]() .
.
Lorsque
![]() , le disque unité, ces questions ont été
abordées principalement pour
, le disque unité, ces questions ont été
abordées principalement pour ![]() , pour la mesure de Lebesgue dans
[3,4], et pour des mesures
, pour la mesure de Lebesgue dans
[3,4], et pour des mesures ![]() particulières par
Imen Fellah dans son rapport de DEA [5]. Des résultats
encourageants, aux plans théorique, algorithmique et numérique
ont été obtenus, de nombreux aspects restent à traiter, qui
constitueront la thèse de Mlle Fellah.
particulières par
Imen Fellah dans son rapport de DEA [5]. Des résultats
encourageants, aux plans théorique, algorithmique et numérique
ont été obtenus, de nombreux aspects restent à traiter, qui
constitueront la thèse de Mlle Fellah.
Les essais numériques dans
![]() seront tout d'abord
poursuivis, face à différents types de singularités,
afin de mieux cerner le rôle de
seront tout d'abord
poursuivis, face à différents types de singularités,
afin de mieux cerner le rôle de ![]() .
.
La pondération ![]() permet de prendre en compte la présence
de singularités au niveau de la géométrie ou des conditions aux
limites que, dans l'état actuel des choses, l'on doit supposer connues a
priori afin de choisir
permet de prendre en compte la présence
de singularités au niveau de la géométrie ou des conditions aux
limites que, dans l'état actuel des choses, l'on doit supposer connues a
priori afin de choisir ![]() .
Cette situation n'est toutefois que rarement rencontrée.
Il convient donc d'imaginer des
méthodes permettant d'effectuer un ``bon'' choix de
.
Cette situation n'est toutefois que rarement rencontrée.
Il convient donc d'imaginer des
méthodes permettant d'effectuer un ``bon'' choix de ![]() depuis les
données disponibles, avant de
prendre appui sur celles-ci pour reconstruire les données
manquantes dans
depuis les
données disponibles, avant de
prendre appui sur celles-ci pour reconstruire les données
manquantes dans
![]() .
On pourra ensuite
appliquer ces méthodes d'extension à la résolution de
certains problèmes inverses d'identification de paramètres et de
géométries inconnues.
.
On pourra ensuite
appliquer ces méthodes d'extension à la résolution de
certains problèmes inverses d'identification de paramètres et de
géométries inconnues.
Par ailleurs, Imen Fellah poursuivra l'étude et la mise en øeuvre
d'un algorithme de
résolution des (PEB) dans
![]() , la contrainte
portant alors
sur le module de l'approximant.
Dans cet ordre d'idées, la prise en compte dans (PEB) de
contraintes différentes sur l'approximant est à envisager, un algorithme
étant déja disponible dans
, la contrainte
portant alors
sur le module de l'approximant.
Dans cet ordre d'idées, la prise en compte dans (PEB) de
contraintes différentes sur l'approximant est à envisager, un algorithme
étant déja disponible dans
![]() (pour la mesure de Lebesgue)
avec contrainte sur
(pour la mesure de Lebesgue)
avec contrainte sur
![]() .
.
Notons que la présence et la recherche de singularités à l'intérieur
de ![]() peuvent être couplées à ce travail (approximation méromorphe
ou rationnelle), comme dans [1,2].
peuvent être couplées à ce travail (approximation méromorphe
ou rationnelle), comme dans [1,2].
L'obtention de résultats de stabilité pour des problèmes inverses
de type (PR) ou géométriques
est aussi à l'ordre du jour, à l'aide de résultats de
contrôle de la norme des fonctions lisses de
![]() .
.
L'utilisation de la pondération ![]() en vue de modéliser des opérateurs
elliptiques plus généraux (conductivité variable, par exemple)
est - elle aussi - à l'étude et peut constituer l'une des facettes de ce
sujet.
en vue de modéliser des opérateurs
elliptiques plus généraux (conductivité variable, par exemple)
est - elle aussi - à l'étude et peut constituer l'une des facettes de ce
sujet.
Slim Chaabane, maître assistant à la Faculté des Sciences de Sfax et chercheur au LAMSIN, participera à l'encadrement effectif de cette thèse.