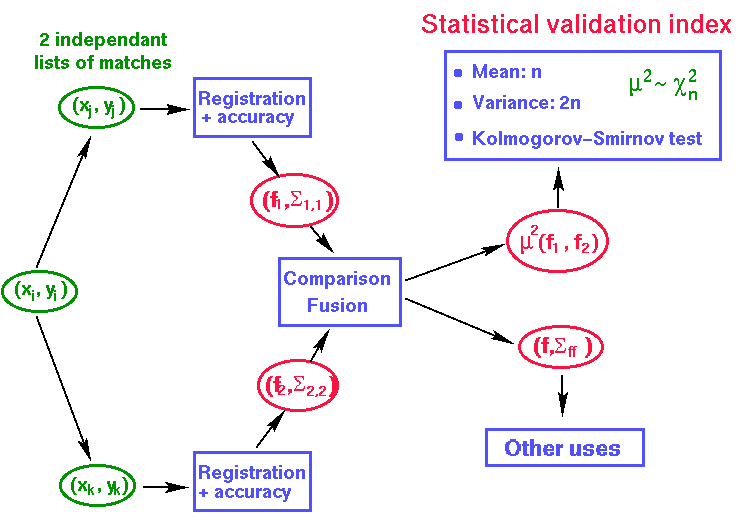
From a list of matched features, we are able to compute the (rigid) transformation that register them, the uncertainty on this transformation, and an estimation of the noise on features.
The question is now: can we trust the registration uncertainty ?
The basic idea to verify this is to seperate (randomly)
the list of matches into two independant lists and compute two independant
estimates of the same transformation along with their uncertainty.
If the computed uncertainties are correct (and under the Gaussian assumption),
the mahalanobis distance of the two independant estimates should follow
a 
(for rigid
transformations). This can be verified with several samples by comparing
the empirical and theoretical mean values and variances (sould be 6 and
12 for a ) or
by comparing the empirical and theoretical distributions using a Kolmogorov-Smirnov
test.
[ Back to uncertainty
in registration for medical imaging ] 