|
|
VARIATIONAL METHODS and PDE's FOR VISION
|
| |
A Variational Framework for Active and Adaptative Segmentation of Vector Valued Images
|
|
|
 During the last few years, many efforts have been done in integrating
different informations in a variational framework to segment
images. Recent works on curve propagation were able to incorporate
stochastic informations [14,10] and prior knowledge on shapes
[3,11]. The information inserted in these studies is most of the time
extracted offline. Meanwhile, other approaches have proposed to
extract region information during the segmentation process itself
[2,4,13]. Following these new approaches and extending the work in
[10] to vector-valued images, we propose in this paper an entirely
variational framework to approach the segmentation problem. Both, the
image partition and the statistical parameters for each region are
unkown. After a brief reminder on recent segmenting methods, we will
present a variational formulation obtained from a bayesian
model. After that, we will show two different differentiations driving
to the same evolution equations. Detailed studies on gray and color
images of the 2-phase case will follow. And we will finish on an
application to tracking which shows benefits of our dynamical
framework.
WMVC'02 Article INRIA Research Report
During the last few years, many efforts have been done in integrating
different informations in a variational framework to segment
images. Recent works on curve propagation were able to incorporate
stochastic informations [14,10] and prior knowledge on shapes
[3,11]. The information inserted in these studies is most of the time
extracted offline. Meanwhile, other approaches have proposed to
extract region information during the segmentation process itself
[2,4,13]. Following these new approaches and extending the work in
[10] to vector-valued images, we propose in this paper an entirely
variational framework to approach the segmentation problem. Both, the
image partition and the statistical parameters for each region are
unkown. After a brief reminder on recent segmenting methods, we will
present a variational formulation obtained from a bayesian
model. After that, we will show two different differentiations driving
to the same evolution equations. Detailed studies on gray and color
images of the 2-phase case will follow. And we will finish on an
application to tracking which shows benefits of our dynamical
framework.
WMVC'02 Article INRIA Research Report
|
| |
Constrained Flows of Matrix-Valued Functions : Application to Diffusion Tensor Regularization
|
|
|
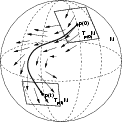 Nonlinear diffusion equations are now widely used to restore and
enhance images. They allow to eliminate noise and artifacts while
preserving large global features, such as object contours. In this
context, we propose a differential-geometric framework to define
regularizing PDEs acting on manifold constrained datasets. We consider
the case of images taking value into matrix manifolds defined by
orthogonal and spectral constraints. We directly incorporate the
geometry and natural metric of the underlying configuration space
(viewed as a Lie group or a homogeneous space) in the design of the
corresponding flows. Our numerical implementation relies on
structure-preserving integrators that respect intrinsically the
constraints geometry. This approach was applied to the anisotropic
smoothing of diffusion tensor volumes in medical imaging.
ECCV'02 Article
Nonlinear diffusion equations are now widely used to restore and
enhance images. They allow to eliminate noise and artifacts while
preserving large global features, such as object contours. In this
context, we propose a differential-geometric framework to define
regularizing PDEs acting on manifold constrained datasets. We consider
the case of images taking value into matrix manifolds defined by
orthogonal and spectral constraints. We directly incorporate the
geometry and natural metric of the underlying configuration space
(viewed as a Lie group or a homogeneous space) in the design of the
corresponding flows. Our numerical implementation relies on
structure-preserving integrators that respect intrinsically the
constraints geometry. This approach was applied to the anisotropic
smoothing of diffusion tensor volumes in medical imaging.
ECCV'02 Article
|
| |
Regularization of DT-MRI Diffusion Tensor Fields with Constraint Preservation
|
|
|
 We address the problem of regularizing fields of diffusion tensors
(i.e symmetric and positive-definite matrices) using PDE's and
variational tools. We consider the minimization of a general
regularizing functional under orthonormal constraints, introduced with
Lagrange multipliers. Accurate numerical schemes are then provided
and we compare this approach with a classical reprojection-step
method. The application of interest considered here is the
regularization of noisy DT-MRI images, in order to construct a
coherent fiber network of the whitte matter.
CVPR'01 Article
We address the problem of regularizing fields of diffusion tensors
(i.e symmetric and positive-definite matrices) using PDE's and
variational tools. We consider the minimization of a general
regularizing functional under orthonormal constraints, introduced with
Lagrange multipliers. Accurate numerical schemes are then provided
and we compare this approach with a classical reprojection-step
method. The application of interest considered here is the
regularization of noisy DT-MRI images, in order to construct a
coherent fiber network of the whitte matter.
CVPR'01 Article
|
| |
Regularization of orthonormal vector sets using coupled PDE's
|
|
|
 This work proposes a variational based approach to regularize fields
of orthonormal vector sets, using constraint-preserving anisotropic
diffusion PDE's. Each point of these fields is defined by multiple
orthogonal and unitary vectors and can indeed represent a lot of
interesting orientation features such direction vectors or orthogonal
matrices (among other examples). We first develop a general
variational framework that solves this regularization problem, thanks
to a constrained minimization of Phi-functionals. This leads to a set
of coupled vector-valued PDE's preserving the orthonormal
constraints. Then, we focus on particular applications of this general
framework, including the restoration of noisy direction fields, noisy
chromaticity color images, estimated camera motion and DT-MRI
(Diffusion Tensor MRI) datasets. First, presented at VLSM'01
Workshop, Vancouver/Canada, July 13, 2001
VLSM'01 Article
IJCV'02 Article
RFIA'02 - In French
This work proposes a variational based approach to regularize fields
of orthonormal vector sets, using constraint-preserving anisotropic
diffusion PDE's. Each point of these fields is defined by multiple
orthogonal and unitary vectors and can indeed represent a lot of
interesting orientation features such direction vectors or orthogonal
matrices (among other examples). We first develop a general
variational framework that solves this regularization problem, thanks
to a constrained minimization of Phi-functionals. This leads to a set
of coupled vector-valued PDE's preserving the orthonormal
constraints. Then, we focus on particular applications of this general
framework, including the restoration of noisy direction fields, noisy
chromaticity color images, estimated camera motion and DT-MRI
(Diffusion Tensor MRI) datasets. First, presented at VLSM'01
Workshop, Vancouver/Canada, July 13, 2001
VLSM'01 Article
IJCV'02 Article
RFIA'02 - In French
|
| |
Constrained and Unconstrained PDEs for Vector Image Restoration
|
|
|
 Here, we propose a new vector image restoration PDE which removes
the noise and enhances blurred vector contours, thanks to a
vector generalisation of scalar $\Phi$-function diffusions and shock filters.
A local and geometric approach is proposed, which uses pertinent vector
informations. Finally, we extend this equation to constrained norm evolutions,
in order to restore direction fields and chromaticity noise on color images.-
Presented at SCIA'01 Conference, Bergen/Norway, 11-14 Jun 2001 -
SCIA'01 Article
IEEE Signal Processing Magazine 2002
Here, we propose a new vector image restoration PDE which removes
the noise and enhances blurred vector contours, thanks to a
vector generalisation of scalar $\Phi$-function diffusions and shock filters.
A local and geometric approach is proposed, which uses pertinent vector
informations. Finally, we extend this equation to constrained norm evolutions,
in order to restore direction fields and chromaticity noise on color images.-
Presented at SCIA'01 Conference, Bergen/Norway, 11-14 Jun 2001 -
SCIA'01 Article
IEEE Signal Processing Magazine 2002
|
|
|
Geodesic Active Regions for Supervised Texture Segmentation
|
|
|
 In this work, we propose a new model for supervised texture
segmentation under a region/boundary-based curve propagation model.
We pursue two main objectives; the first is to propose a
complete framework for texture analysis and modeling that combines
existing approaches in this domain and provides a reliable texture
description model with a limited set of parameters. This model must be
general to describe a wide variety of texture patterns. The second
objective is to unify boundary-based and region-based segmentation
using a variational approach.
International Journal on Computer Vision, Volume 50, Number 3, pages 237-252, Dec. 2002 Article
In this work, we propose a new model for supervised texture
segmentation under a region/boundary-based curve propagation model.
We pursue two main objectives; the first is to propose a
complete framework for texture analysis and modeling that combines
existing approaches in this domain and provides a reliable texture
description model with a limited set of parameters. This model must be
general to describe a wide variety of texture patterns. The second
objective is to unify boundary-based and region-based segmentation
using a variational approach.
International Journal on Computer Vision, Volume 50, Number 3, pages 237-252, Dec. 2002 Article
|
|
|
Coupled Geodesic Active Regions for Image Segmentation
|
|
|
 A novel variational method that unify boundary and region-based
segmentation modules under the Geodesic Active Region framework is
presented. A statistical analysis over the observed density function
using a mixture of Gaussian elements, is first used to indicate the
number of the different regions and their intensity properties. Then,
the boundary information is determined using a probabilistic edge
detector, while the region information is given directly from the
observed image using the conditional probability density functions of
the mixture model. The defined objective function is minimized using a
gradient-descent method implemented through the use of the level-set
method. The changes of topology of the curves during their evolution
are naturally handled thanks to the level set implementation, while a
coupled multi-phase propagation is adopted that increases the
robustness and the convergence rate by introducing a coupled system of
equations for the different level set functions.
ECCV'2000 Article
A novel variational method that unify boundary and region-based
segmentation modules under the Geodesic Active Region framework is
presented. A statistical analysis over the observed density function
using a mixture of Gaussian elements, is first used to indicate the
number of the different regions and their intensity properties. Then,
the boundary information is determined using a probabilistic edge
detector, while the region information is given directly from the
observed image using the conditional probability density functions of
the mixture model. The defined objective function is minimized using a
gradient-descent method implemented through the use of the level-set
method. The changes of topology of the curves during their evolution
are naturally handled thanks to the level set implementation, while a
coupled multi-phase propagation is adopted that increases the
robustness and the convergence rate by introducing a coupled system of
equations for the different level set functions.
ECCV'2000 Article
|
|
|
Geodesic Active Contours/Regions for Detection and Tracking
|
|
|
 In this work, we propose a new framework for tracking multiple
non-rigid moving objects using a region/boundary-based curve
propagation model.The objective of this work is to provide a complete
tracking model that can deal successfully with the most difficult
tracking cases, i.e non-rigid objects and non-rigid movements.
In this work, we propose a new framework for tracking multiple
non-rigid moving objects using a region/boundary-based curve
propagation model.The objective of this work is to provide a complete
tracking model that can deal successfully with the most difficult
tracking cases, i.e non-rigid objects and non-rigid movements.
|
|
|
PDE's for Color Image Restoration
|
|
|
 Coupled PDE's are introduced for vector image restoration and applyed
to color images. Diffusion-reaction terms are developed to deal with
both the debluring and denoising problems.
Slides of the thesis presentation
Coupled PDE's are introduced for vector image restoration and applyed
to color images. Diffusion-reaction terms are developed to deal with
both the debluring and denoising problems.
Slides of the thesis presentation
|
|
|
Image and Sequence Enhanchement, Restoration and Deblurring via PDE
|
|
|
 A
In this work, we illustrate the results obtained using a variational approach
devised for the purpose of image restoration with the constraint to
preserve the edges within the original image.the restoration problem is set
as a regularization and minimization of a non quadratic functional A
In this work, we illustrate the results obtained using a variational approach
devised for the purpose of image restoration with the constraint to
preserve the edges within the original image.the restoration problem is set
as a regularization and minimization of a non quadratic functional
|
|
|
Dense Disparity Map Estimation Respecting Image Discontinuities
|
|
|
 We propose an energy based method to estimate a dense disparity map
between 3 images while preserving its discontinuities accordingly to
the image boundaries that may be present. We first derive a simplified
expression for the disparity that allows us to easily estimate it from
a stereo pair of images. Dicsontinuities are preserved using a
regularization constraint term based on the Nagel and Enkelmann
operator to better estimate and preserve the discontinuities. We
assume that the epipolar geometry is known, and we include this
information in the energy model. We derive the associated
Euler-Lagrange equation and we approach the solution of the underlying
partial differential equation using a gradient descent method. In
order to reduce the risk to be trapped within some irrelevant local
minima, we use a focusing strategy based on a linear Gaussian scale
space.
We propose an energy based method to estimate a dense disparity map
between 3 images while preserving its discontinuities accordingly to
the image boundaries that may be present. We first derive a simplified
expression for the disparity that allows us to easily estimate it from
a stereo pair of images. Dicsontinuities are preserved using a
regularization constraint term based on the Nagel and Enkelmann
operator to better estimate and preserve the discontinuities. We
assume that the epipolar geometry is known, and we include this
information in the energy model. We derive the associated
Euler-Lagrange equation and we approach the solution of the underlying
partial differential equation using a gradient descent method. In
order to reduce the risk to be trapped within some irrelevant local
minima, we use a focusing strategy based on a linear Gaussian scale
space.
|
|
|
Dense Depth Recovery from Stereo: A Minimization and Regularization Approach
|
|
|
 We present a variational approach to dense stereo reconstruction which combines
powerful tools such as regularization and multi-scale processing to
estimate directly depth from a number of stereo images, while
preserving depth discontinuities. The problem is set as a
regularization and minimization of a non quadratic functional.
We present a variational approach to dense stereo reconstruction which combines
powerful tools such as regularization and multi-scale processing to
estimate directly depth from a number of stereo images, while
preserving depth discontinuities. The problem is set as a
regularization and minimization of a non quadratic functional.
|
|
|
A PDE-based Level Set approach for Stereovision
|
|
|
 In this work, we provide a totally new approach to deal with the important problem
of matching 2D curves from a stereo pair of images
We use the framework of energy minimization and express our problem as a
geodesic active contour based approach.
In this work, we provide a totally new approach to deal with the important problem
of matching 2D curves from a stereo pair of images
We use the framework of energy minimization and express our problem as a
geodesic active contour based approach.
|
|
3D Vision and Geometry
|
|
|
Autocalibration Using an SVD-Based Simplification of the Kruppa Equations
|
|
|
 Autocalibration in the case of constant and varying intrinsic parameters.
This paper deals with a fundamental problem in motion and stereo
analysis, namely that of determining the camera intrinsic calibration
parameters. Two methods are proposed that follows the autocalibration
paradigm, according to which calibration is achieved not with the aid
of a calibration pattern but by observing a number of image features
in a set of successive images. The two proposed methods relie upon the
Singular Value Decomposition of the fundamental matrix, which leads to
a particularly simple form of the Kruppa equations.
Autocalibration in the case of constant and varying intrinsic parameters are
considered.
Experimental results from extensive simulations and several image
sequences, taking into account the uncertainty of the measurements,
demonstrate the effectiveness of the proposed methods in accurately
estimating the intrinsic calibration matrices. It is also
shown that the computed intrinsic calibration matrices are sufficient
for recovering 3D measurement, 3 motion and 3D Recosntruction from
uncalibrated images.
Autocalibration in the case of constant and varying intrinsic parameters.
This paper deals with a fundamental problem in motion and stereo
analysis, namely that of determining the camera intrinsic calibration
parameters. Two methods are proposed that follows the autocalibration
paradigm, according to which calibration is achieved not with the aid
of a calibration pattern but by observing a number of image features
in a set of successive images. The two proposed methods relie upon the
Singular Value Decomposition of the fundamental matrix, which leads to
a particularly simple form of the Kruppa equations.
Autocalibration in the case of constant and varying intrinsic parameters are
considered.
Experimental results from extensive simulations and several image
sequences, taking into account the uncertainty of the measurements,
demonstrate the effectiveness of the proposed methods in accurately
estimating the intrinsic calibration matrices. It is also
shown that the computed intrinsic calibration matrices are sufficient
for recovering 3D measurement, 3 motion and 3D Recosntruction from
uncalibrated images.
|
|
Early Vision and Model Based Approaches
|
|
|
Recovering and Characterizing Image Features with a model-based approach
|
|
|
 Edges, corners and vertices are strong and useful features in computer
vision. The work illustreted here deals with the development of an
efficient model based approach in order to detect and characterize
precisely these important features. The key of our approach is first
to propose some efficient models associated to each of these features
and second to efficiently extract and characterize these features
directly from the image.
Edges, corners and vertices are strong and useful features in computer
vision. The work illustreted here deals with the development of an
efficient model based approach in order to detect and characterize
precisely these important features. The key of our approach is first
to propose some efficient models associated to each of these features
and second to efficiently extract and characterize these features
directly from the image.
|
|
|
A Model Based Method for Characterization and
Location of Curved Image Features
|
|
|
 This work deals with the development of a parametric model based
method to locate and characterize precisely important curved features
such as ellipses and B-splines based curves. The method uses all the
grey level information of the pixels contained within a window around
the feature of interest and produces the complete parametric model
that best approximates in a mean-square sense the observed grey level
image intensities within the working area.
This work deals with the development of a parametric model based
method to locate and characterize precisely important curved features
such as ellipses and B-splines based curves. The method uses all the
grey level information of the pixels contained within a window around
the feature of interest and produces the complete parametric model
that best approximates in a mean-square sense the observed grey level
image intensities within the working area.
|
|
|
On Parametric Deformable Models in Computer Vision: 2D Curve Tracking
|
|
|
 Feature Extraction Using Parametric Snakes - Energy Based Methods for 2D Curve Tracking and Applications
Feature Extraction Using Parametric Snakes - Energy Based Methods for 2D Curve Tracking and Applications
|
|
|
On Parametric Deformable Models in Computer Vision: Refinement of 3D Curves
|
|
|
 Stereo Matching, Reconstruction and Refinement of 3-{D} Curves Using Deformable Contours - Energy Based Methods
for Ronstruction, and Refinement of 3{D} Curves and Applications
Stereo Matching, Reconstruction and Refinement of 3-{D} Curves Using Deformable Contours - Energy Based Methods
for Ronstruction, and Refinement of 3{D} Curves and Applications
|
|
|
On Image Features Extraction
|
|
|
 Using Canny's Criteria to Derive a Recursively Implemented Optimal Edge Detector - Fast Algorithms for Low-Level Vision. - An Efficient Method to Build an Early Image Description -
- A Computational Approach For Corner And Vertex Detection etc..
Using Canny's Criteria to Derive a Recursively Implemented Optimal Edge Detector - Fast Algorithms for Low-Level Vision. - An Efficient Method to Build an Early Image Description -
- A Computational Approach For Corner And Vertex Detection etc..
|
|
|
|


 During the last few years, many efforts have been done in integrating
different informations in a variational framework to segment
images. Recent works on curve propagation were able to incorporate
stochastic informations [14,10] and prior knowledge on shapes
[3,11]. The information inserted in these studies is most of the time
extracted offline. Meanwhile, other approaches have proposed to
extract region information during the segmentation process itself
[2,4,13]. Following these new approaches and extending the work in
[10] to vector-valued images, we propose in this paper an entirely
variational framework to approach the segmentation problem. Both, the
image partition and the statistical parameters for each region are
unkown. After a brief reminder on recent segmenting methods, we will
present a variational formulation obtained from a bayesian
model. After that, we will show two different differentiations driving
to the same evolution equations. Detailed studies on gray and color
images of the 2-phase case will follow. And we will finish on an
application to tracking which shows benefits of our dynamical
framework.
During the last few years, many efforts have been done in integrating
different informations in a variational framework to segment
images. Recent works on curve propagation were able to incorporate
stochastic informations [14,10] and prior knowledge on shapes
[3,11]. The information inserted in these studies is most of the time
extracted offline. Meanwhile, other approaches have proposed to
extract region information during the segmentation process itself
[2,4,13]. Following these new approaches and extending the work in
[10] to vector-valued images, we propose in this paper an entirely
variational framework to approach the segmentation problem. Both, the
image partition and the statistical parameters for each region are
unkown. After a brief reminder on recent segmenting methods, we will
present a variational formulation obtained from a bayesian
model. After that, we will show two different differentiations driving
to the same evolution equations. Detailed studies on gray and color
images of the 2-phase case will follow. And we will finish on an
application to tracking which shows benefits of our dynamical
framework.  We address the problem of regularizing fields of diffusion tensors
(i.e symmetric and positive-definite matrices) using PDE's and
variational tools. We consider the minimization of a general
regularizing functional under orthonormal constraints, introduced with
Lagrange multipliers. Accurate numerical schemes are then provided
and we compare this approach with a classical reprojection-step
method. The application of interest considered here is the
regularization of noisy DT-MRI images, in order to construct a
coherent fiber network of the whitte matter.
We address the problem of regularizing fields of diffusion tensors
(i.e symmetric and positive-definite matrices) using PDE's and
variational tools. We consider the minimization of a general
regularizing functional under orthonormal constraints, introduced with
Lagrange multipliers. Accurate numerical schemes are then provided
and we compare this approach with a classical reprojection-step
method. The application of interest considered here is the
regularization of noisy DT-MRI images, in order to construct a
coherent fiber network of the whitte matter.
 This work proposes a variational based approach to regularize fields
of orthonormal vector sets, using constraint-preserving anisotropic
diffusion PDE's. Each point of these fields is defined by multiple
orthogonal and unitary vectors and can indeed represent a lot of
interesting orientation features such direction vectors or orthogonal
matrices (among other examples). We first develop a general
variational framework that solves this regularization problem, thanks
to a constrained minimization of Phi-functionals. This leads to a set
of coupled vector-valued PDE's preserving the orthonormal
constraints. Then, we focus on particular applications of this general
framework, including the restoration of noisy direction fields, noisy
chromaticity color images, estimated camera motion and DT-MRI
(Diffusion Tensor MRI) datasets. First, presented at VLSM'01
Workshop, Vancouver/Canada, July 13, 2001
This work proposes a variational based approach to regularize fields
of orthonormal vector sets, using constraint-preserving anisotropic
diffusion PDE's. Each point of these fields is defined by multiple
orthogonal and unitary vectors and can indeed represent a lot of
interesting orientation features such direction vectors or orthogonal
matrices (among other examples). We first develop a general
variational framework that solves this regularization problem, thanks
to a constrained minimization of Phi-functionals. This leads to a set
of coupled vector-valued PDE's preserving the orthonormal
constraints. Then, we focus on particular applications of this general
framework, including the restoration of noisy direction fields, noisy
chromaticity color images, estimated camera motion and DT-MRI
(Diffusion Tensor MRI) datasets. First, presented at VLSM'01
Workshop, Vancouver/Canada, July 13, 2001
 Here, we propose a new vector image restoration PDE which removes
the noise and enhances blurred vector contours, thanks to a
vector generalisation of scalar $\Phi$-function diffusions and shock filters.
A local and geometric approach is proposed, which uses pertinent vector
informations. Finally, we extend this equation to constrained norm evolutions,
in order to restore direction fields and chromaticity noise on color images.-
Presented at SCIA'01 Conference, Bergen/Norway, 11-14 Jun 2001 -
Here, we propose a new vector image restoration PDE which removes
the noise and enhances blurred vector contours, thanks to a
vector generalisation of scalar $\Phi$-function diffusions and shock filters.
A local and geometric approach is proposed, which uses pertinent vector
informations. Finally, we extend this equation to constrained norm evolutions,
in order to restore direction fields and chromaticity noise on color images.-
Presented at SCIA'01 Conference, Bergen/Norway, 11-14 Jun 2001 -
 In this work, we propose a new model for supervised texture
segmentation under a region/boundary-based curve propagation model.
We pursue two main objectives; the first is to propose a
complete framework for texture analysis and modeling that combines
existing approaches in this domain and provides a reliable texture
description model with a limited set of parameters. This model must be
general to describe a wide variety of texture patterns. The second
objective is to unify boundary-based and region-based segmentation
using a variational approach.
In this work, we propose a new model for supervised texture
segmentation under a region/boundary-based curve propagation model.
We pursue two main objectives; the first is to propose a
complete framework for texture analysis and modeling that combines
existing approaches in this domain and provides a reliable texture
description model with a limited set of parameters. This model must be
general to describe a wide variety of texture patterns. The second
objective is to unify boundary-based and region-based segmentation
using a variational approach.
 A novel variational method that unify boundary and region-based
segmentation modules under the Geodesic Active Region framework is
presented. A statistical analysis over the observed density function
using a mixture of Gaussian elements, is first used to indicate the
number of the different regions and their intensity properties. Then,
the boundary information is determined using a probabilistic edge
detector, while the region information is given directly from the
observed image using the conditional probability density functions of
the mixture model. The defined objective function is minimized using a
gradient-descent method implemented through the use of the level-set
method. The changes of topology of the curves during their evolution
are naturally handled thanks to the level set implementation, while a
coupled multi-phase propagation is adopted that increases the
robustness and the convergence rate by introducing a coupled system of
equations for the different level set functions.
A novel variational method that unify boundary and region-based
segmentation modules under the Geodesic Active Region framework is
presented. A statistical analysis over the observed density function
using a mixture of Gaussian elements, is first used to indicate the
number of the different regions and their intensity properties. Then,
the boundary information is determined using a probabilistic edge
detector, while the region information is given directly from the
observed image using the conditional probability density functions of
the mixture model. The defined objective function is minimized using a
gradient-descent method implemented through the use of the level-set
method. The changes of topology of the curves during their evolution
are naturally handled thanks to the level set implementation, while a
coupled multi-phase propagation is adopted that increases the
robustness and the convergence rate by introducing a coupled system of
equations for the different level set functions.
 In this work, we propose a new framework for tracking multiple
non-rigid moving objects using a region/boundary-based curve
propagation model.The objective of this work is to provide a complete
tracking model that can deal successfully with the most difficult
tracking cases, i.e non-rigid objects and non-rigid movements.
In this work, we propose a new framework for tracking multiple
non-rigid moving objects using a region/boundary-based curve
propagation model.The objective of this work is to provide a complete
tracking model that can deal successfully with the most difficult
tracking cases, i.e non-rigid objects and non-rigid movements.
 Coupled PDE's are introduced for vector image restoration and applyed
to color images. Diffusion-reaction terms are developed to deal with
both the debluring and denoising problems.
Coupled PDE's are introduced for vector image restoration and applyed
to color images. Diffusion-reaction terms are developed to deal with
both the debluring and denoising problems.
 A
In this work, we illustrate the results obtained using a variational approach
devised for the purpose of image restoration with the constraint to
preserve the edges within the original image.the restoration problem is set
as a regularization and minimization of a non quadratic functional
A
In this work, we illustrate the results obtained using a variational approach
devised for the purpose of image restoration with the constraint to
preserve the edges within the original image.the restoration problem is set
as a regularization and minimization of a non quadratic functional
 We propose an energy based method to estimate a dense disparity map
between 3 images while preserving its discontinuities accordingly to
the image boundaries that may be present. We first derive a simplified
expression for the disparity that allows us to easily estimate it from
a stereo pair of images. Dicsontinuities are preserved using a
regularization constraint term based on the Nagel and Enkelmann
operator to better estimate and preserve the discontinuities. We
assume that the epipolar geometry is known, and we include this
information in the energy model. We derive the associated
Euler-Lagrange equation and we approach the solution of the underlying
partial differential equation using a gradient descent method. In
order to reduce the risk to be trapped within some irrelevant local
minima, we use a focusing strategy based on a linear Gaussian scale
space.
We propose an energy based method to estimate a dense disparity map
between 3 images while preserving its discontinuities accordingly to
the image boundaries that may be present. We first derive a simplified
expression for the disparity that allows us to easily estimate it from
a stereo pair of images. Dicsontinuities are preserved using a
regularization constraint term based on the Nagel and Enkelmann
operator to better estimate and preserve the discontinuities. We
assume that the epipolar geometry is known, and we include this
information in the energy model. We derive the associated
Euler-Lagrange equation and we approach the solution of the underlying
partial differential equation using a gradient descent method. In
order to reduce the risk to be trapped within some irrelevant local
minima, we use a focusing strategy based on a linear Gaussian scale
space.
 We present a variational approach to dense stereo reconstruction which combines
powerful tools such as regularization and multi-scale processing to
estimate directly depth from a number of stereo images, while
preserving depth discontinuities. The problem is set as a
regularization and minimization of a non quadratic functional.
We present a variational approach to dense stereo reconstruction which combines
powerful tools such as regularization and multi-scale processing to
estimate directly depth from a number of stereo images, while
preserving depth discontinuities. The problem is set as a
regularization and minimization of a non quadratic functional.
 In this work, we provide a totally new approach to deal with the important problem
of matching 2D curves from a stereo pair of images
We use the framework of energy minimization and express our problem as a
geodesic active contour based approach.
In this work, we provide a totally new approach to deal with the important problem
of matching 2D curves from a stereo pair of images
We use the framework of energy minimization and express our problem as a
geodesic active contour based approach.
 Autocalibration in the case of constant and varying intrinsic parameters.
This paper deals with a fundamental problem in motion and stereo
analysis, namely that of determining the camera intrinsic calibration
parameters. Two methods are proposed that follows the autocalibration
paradigm, according to which calibration is achieved not with the aid
of a calibration pattern but by observing a number of image features
in a set of successive images. The two proposed methods relie upon the
Singular Value Decomposition of the fundamental matrix, which leads to
a particularly simple form of the Kruppa equations.
Autocalibration in the case of constant and varying intrinsic parameters are
considered.
Experimental results from extensive simulations and several image
sequences, taking into account the uncertainty of the measurements,
demonstrate the effectiveness of the proposed methods in accurately
estimating the intrinsic calibration matrices. It is also
shown that the computed intrinsic calibration matrices are sufficient
for recovering 3D measurement, 3 motion and 3D Recosntruction from
uncalibrated images.
Autocalibration in the case of constant and varying intrinsic parameters.
This paper deals with a fundamental problem in motion and stereo
analysis, namely that of determining the camera intrinsic calibration
parameters. Two methods are proposed that follows the autocalibration
paradigm, according to which calibration is achieved not with the aid
of a calibration pattern but by observing a number of image features
in a set of successive images. The two proposed methods relie upon the
Singular Value Decomposition of the fundamental matrix, which leads to
a particularly simple form of the Kruppa equations.
Autocalibration in the case of constant and varying intrinsic parameters are
considered.
Experimental results from extensive simulations and several image
sequences, taking into account the uncertainty of the measurements,
demonstrate the effectiveness of the proposed methods in accurately
estimating the intrinsic calibration matrices. It is also
shown that the computed intrinsic calibration matrices are sufficient
for recovering 3D measurement, 3 motion and 3D Recosntruction from
uncalibrated images.
 Edges, corners and vertices are strong and useful features in computer
vision. The work illustreted here deals with the development of an
efficient model based approach in order to detect and characterize
precisely these important features. The key of our approach is first
to propose some efficient models associated to each of these features
and second to efficiently extract and characterize these features
directly from the image.
Edges, corners and vertices are strong and useful features in computer
vision. The work illustreted here deals with the development of an
efficient model based approach in order to detect and characterize
precisely these important features. The key of our approach is first
to propose some efficient models associated to each of these features
and second to efficiently extract and characterize these features
directly from the image.
 This work deals with the development of a parametric model based
method to locate and characterize precisely important curved features
such as ellipses and B-splines based curves. The method uses all the
grey level information of the pixels contained within a window around
the feature of interest and produces the complete parametric model
that best approximates in a mean-square sense the observed grey level
image intensities within the working area.
This work deals with the development of a parametric model based
method to locate and characterize precisely important curved features
such as ellipses and B-splines based curves. The method uses all the
grey level information of the pixels contained within a window around
the feature of interest and produces the complete parametric model
that best approximates in a mean-square sense the observed grey level
image intensities within the working area.
 Feature Extraction Using Parametric Snakes - Energy Based Methods for 2D Curve Tracking and Applications
Feature Extraction Using Parametric Snakes - Energy Based Methods for 2D Curve Tracking and Applications
 Stereo Matching, Reconstruction and Refinement of 3-{D} Curves Using Deformable Contours - Energy Based Methods
for Ronstruction, and Refinement of 3{D} Curves and Applications
Stereo Matching, Reconstruction and Refinement of 3-{D} Curves Using Deformable Contours - Energy Based Methods
for Ronstruction, and Refinement of 3{D} Curves and Applications
 Using Canny's Criteria to Derive a Recursively Implemented Optimal Edge Detector - Fast Algorithms for Low-Level Vision. - An Efficient Method to Build an Early Image Description -
- A Computational Approach For Corner And Vertex Detection etc..
Using Canny's Criteria to Derive a Recursively Implemented Optimal Edge Detector - Fast Algorithms for Low-Level Vision. - An Efficient Method to Build an Early Image Description -
- A Computational Approach For Corner And Vertex Detection etc..