EDGE DETECTION

Grégoire Malandain

  • Principles
  • Example: 2D edge detection versus 3D edge detection
  • Code
  • Examples obtained with the code
  • Other uses of the code

    • Principles

    Image edges may be defined by:

    Example: 2D edge detection versus 3D edge detection

    In this example, edges are considered to be the maxima of the gradient modulus in the direction of the gradient.

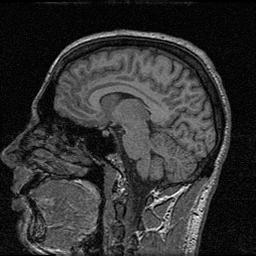
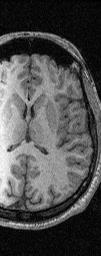
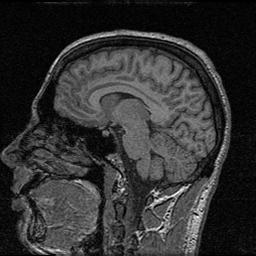
    A sagittal and an axial slice of a 3D MR data volume.

    The edge detection is performed in 2D on each sagittal slice, and the results are collected to form a 3D volume. Edges are superimposed on the original 3D MR data volume. One may notice that the collection of 2D edges is not coherent along the third dimension.


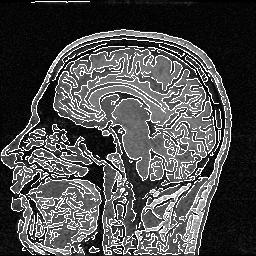
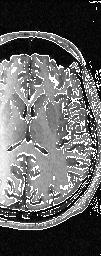
    "2D edges" superimposed on the original 3D MR data volume.

    On the other hand, 3D edges look nicer.


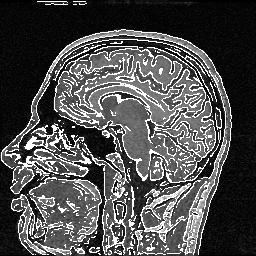
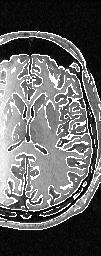
    3D edges superimposed on the original 3D MR data volume.

    Code

    A small library (written in C) allowing 2D or 3D edge detection with recursive filtering (see Recursive filtering and edge tracking: two primary tools for 3-D edge detection, Olivier Monga, Rachid Deriche, Grégoire Malandain, Jean-Pierre Cocquerez Image and Vision Computing, 1991, 9 (4), pp.203--214.) and a connected components extraction tools (which allows hysteresis thresholding) are available for non-commercial uses only.

    Examples obtained with the code

    Original image

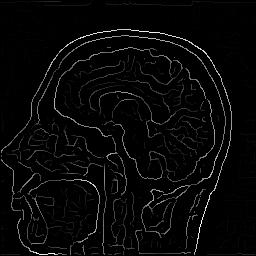
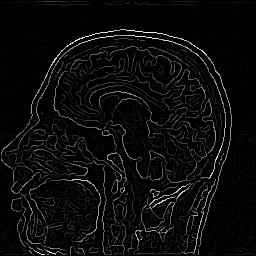
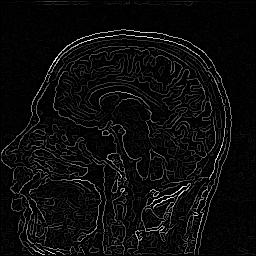
    Edge detection with Deriche's recursive filter (~ exp(-alpha |x|) )
    %test-edges-pnm greg-rmn.pgm greg-rmn.a=alpha.ppm -a alpha
    alpha=0.5 alpha=1.0 alpha=1.5

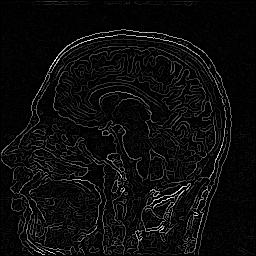
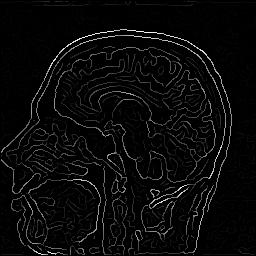
    Edge detection with a recursive approximation of the Gaussian
    %test-edges-pnm greg-rmn.pgm greg-rmn.s=sigma.ppm -s sigma
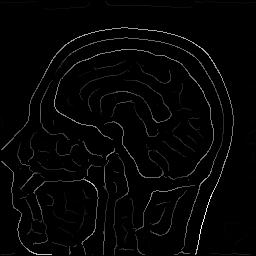    sigma=1.0 sigma=2.0 sigma=5.0

    Hysteresis thresholding on previous results (edge detection with a recursive approximation of the Gaussian)
    low threshold = 10, high threshold = 20, minimal size of connected component = 30
    %test-hyster-pnm greg-rmn.s=sigma.ppm greg-rmn.s=sigma.lt=10.ht=20.ms=30.ppm -lt 10 -ht 20 -ms 30
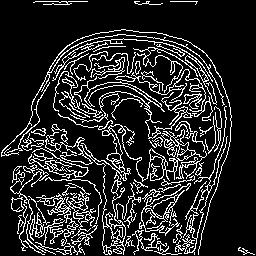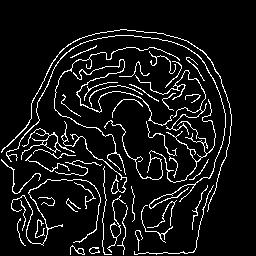    sigma=1.0 sigma=2.0 sigma=5.0

    Other uses of the code

    Although it has be designed for edge detection (and thus performs smoothing and first order derivatives), the filtering part of the code can be used to compute image derivatives up to the second order (e.g. curvatures).
    Grégoire Malandain
    Last modified: Mon Feb 12 15:12:45 MET 2001