Elliptic section
from P. Olver, Pick invariant, in preparation.
| fr > | Section:=[x=0,y=0,u[0,0]=0,u[1,0]=0,u[0,1]=0,u[1,1]=0,u[2,0]=1,u[0,2]=1,u[0,3]=0,u[2,1]=0, u[1,2]=-u[3,0]]:stair(Section); |
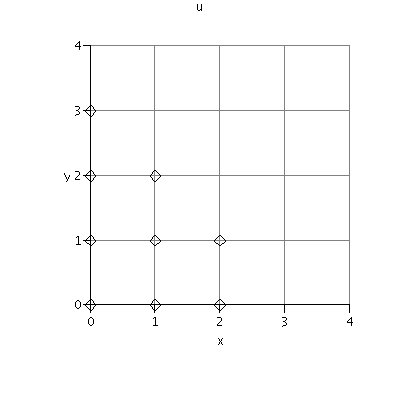
| fr > | C, Invariantizations :=dmf(LieAlg,Section, fr, [op(1..10,Section), u[3,0]=Pk,u[4,0]=e,u[3,1]=d,u[2,2]=c,u[1,3]=12*Pk*S1+3*d,u[0,4]=12*Pk*S2+3*c], 'COM'): |
"Section :"
![[u[0, 3] = 0, u[1, 2] = -u[3, 0], u[2, 1] = 0, u[0, 2] = 1, u[1, 1] = 0, u[2, 0] = 1, u[0, 1] = 0, u[1, 0] = 0, u[0, 0] = 0, y = 0, x = 0]](images/dmf_182.gif){kind=small}
![[u[0, 3] = 0, u[1, 2] = -u[3, 0], u[2, 1] = 0, u[0, 2] = 1, u[1, 1] = 0, u[2, 0] = 1, u[0, 1] = 0, u[1, 0] = 0, u[0, 0] = 0, y = 0, x = 0]](images/dmf_183.gif){kind=small}
"Transversality condition :" u[3 0]
"Invariantizations:"
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[1, 1] = 0, u[2, 0] = 1, u[0, 2] = 1, u[0, 3] = 0, u[2, 1] = 0, u[3, 0] = Pk, u[4, 0] = e, u[3, 1] = d, u[2, 2] = c, u[1, 3] = 12*Pk*S1+3*d, u[0, ...](images/dmf_184.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[1, 1] = 0, u[2, 0] = 1, u[0, 2] = 1, u[0, 3] = 0, u[2, 1] = 0, u[3, 0] = Pk, u[4, 0] = e, u[3, 1] = d, u[2, 2] = c, u[1, 3] = 12*Pk*S1+3*d, u[0, ...](images/dmf_185.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[1, 1] = 0, u[2, 0] = 1, u[0, 2] = 1, u[0, 3] = 0, u[2, 1] = 0, u[3, 0] = Pk, u[4, 0] = e, u[3, 1] = d, u[2, 2] = c, u[1, 3] = 12*Pk*S1+3*d, u[0, ...](images/dmf_186.gif){kind=small}
"Commutation rules"
![[D1, D2] = -1/12*(-u[1, 3]+3*u[3, 1])*D1/u[3, 0]-1/12*(-u[0, 4]+3*u[2, 2])*D2/u[3, 0]](images/dmf_187.gif)
"Syzygies"
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_188.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_189.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_190.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_191.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_192.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_193.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_194.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_195.gif){kind=small}
![[-9*Pk[0, 0]*d[0, 0]-36*Pk[0, 0]^2*S1[0, 0]-4*d[0, 0]*S2[0, 0]-e[0, 0]*S1[0, 0]+3*c[0, 0]*S1[0, 0]-e[0, 1]+d[1, 0], S2[0, 0]*e[0, 0]-3*c[0, 0]*S2[0, 0]+6*Pk[0, 0]^2*S2[0, 0]+3*Pk[0, 0]*c[0, 0]+4*d[0, ...](images/dmf_196.gif){kind=small}
"Syzygies with attempt to eliminate the y's"
![y0[0, 0] = 1/Pk[0, 0]](images/dmf_197.gif){kind=small}
![y1[0, 0] = -Pk[0, 0]](images/dmf_198.gif){kind=small}
![d[1, 0] = 9*Pk[0, 0]*d[0, 0]+36*Pk[0, 0]^2*S1[0, 0]+4*d[0, 0]*S2[0, 0]+e[0, 0]*S1[0, 0]-3*c[0, 0]*S1[0, 0]+e[0, 1]](images/dmf_199.gif){kind=small}
![d[1, 0] = 9*Pk[0, 0]*d[0, 0]+36*Pk[0, 0]^2*S1[0, 0]+4*d[0, 0]*S2[0, 0]+e[0, 0]*S1[0, 0]-3*c[0, 0]*S1[0, 0]+e[0, 1]](images/dmf_200.gif){kind=small}
![c[1, 0] = -S2[0, 0]*e[0, 0]+3*c[0, 0]*S2[0, 0]-6*Pk[0, 0]^2*S2[0, 0]-3*Pk[0, 0]*c[0, 0]-4*d[0, 0]*S1[0, 0]-24*Pk[0, 0]*S1[0, 0]^2+d[0, 1]](images/dmf_201.gif){kind=small}
![c[1, 0] = -S2[0, 0]*e[0, 0]+3*c[0, 0]*S2[0, 0]-6*Pk[0, 0]^2*S2[0, 0]-3*Pk[0, 0]*c[0, 0]-4*d[0, 0]*S1[0, 0]-24*Pk[0, 0]*S1[0, 0]^2+d[0, 1]](images/dmf_202.gif){kind=small}
![c[1, 0] = -S2[0, 0]*e[0, 0]+3*c[0, 0]*S2[0, 0]-6*Pk[0, 0]^2*S2[0, 0]-3*Pk[0, 0]*c[0, 0]-4*d[0, 0]*S1[0, 0]-24*Pk[0, 0]*S1[0, 0]^2+d[0, 1]](images/dmf_203.gif){kind=small}
![Pk[1, 0] = 1/4*e[0, 0]-3/4*c[0, 0]](images/dmf_204.gif){kind=small}
![S1[1, 0] = 1/12*(-8*d[0, 0]*S2[0, 0]-24*Pk[0, 0]*d[0, 0]-96*Pk[0, 0]^2*S1[0, 0]+12*Pk[0, 0]*S1[0, 0]*S2[0, 0]+c[0, 1]-6*e[0, 0]*S1[0, 0]+18*c[0, 0]*S1[0, 0]-3*e[0, 1])/Pk[0, 0]](images/dmf_205.gif){kind=small}
![S1[1, 0] = 1/12*(-8*d[0, 0]*S2[0, 0]-24*Pk[0, 0]*d[0, 0]-96*Pk[0, 0]^2*S1[0, 0]+12*Pk[0, 0]*S1[0, 0]*S2[0, 0]+c[0, 1]-6*e[0, 0]*S1[0, 0]+18*c[0, 0]*S1[0, 0]-3*e[0, 1])/Pk[0, 0]](images/dmf_206.gif){kind=small}
![S1[1, 0] = 1/12*(-8*d[0, 0]*S2[0, 0]-24*Pk[0, 0]*d[0, 0]-96*Pk[0, 0]^2*S1[0, 0]+12*Pk[0, 0]*S1[0, 0]*S2[0, 0]+c[0, 1]-6*e[0, 0]*S1[0, 0]+18*c[0, 0]*S1[0, 0]-3*e[0, 1])/Pk[0, 0]](images/dmf_207.gif){kind=small}
![S2[1, 0] = 5/8*c[0, 0]+S2[0, 0]^2+3/2*Pk[0, 0]*S2[0, 0]+S1[0, 0]^2+1/8*e[0, 0]+S1[0, 1]](images/dmf_208.gif){kind=small}
![Pk[0, 1] = -2*d[0, 0]-9*Pk[0, 0]*S1[0, 0]](images/dmf_209.gif){kind=small}
Can we express [c,d,e], the invariantization of ![[u[2, 2], u[3, 1], u[4, 0]]](images/dmf_210.gif){kind=small}
in terms of ![[a, b, kappa]](images/dmf_211.gif){kind=small}
the invariantizations of
![[1/12*(u[0, 4]-3*u[2, 2])/u[3, 0], -1/12*(u[1, 3]+3*u[3, 1])/u[3, 0], u[3, 0]]](images/dmf_212.gif)
![CC := [characterisable]](images/dmf_213.gif){kind=small}
![c[0, 0] = -a[0, 0]^2-1/2*kappa[1, 0]-b[0, 0]^2-b[0, 1]+a[1, 0]-3/2*kappa[0, 0]*a[0, 0]](images/dmf_214.gif){kind=small}
![d[0, 0] = -1/2*kappa[0, 1]-9/2*kappa[0, 0]*b[0, 0]](images/dmf_215.gif){kind=small}
![e[0, 0] = 5/2*kappa[1, 0]-3*a[0, 0]^2-3*b[0, 0]^2-3*b[0, 1]+3*a[1, 0]-9/2*kappa[0, 0]*a[0, 0]](images/dmf_216.gif){kind=small}
![y0[0, 0] = 1/384/kappa[0, 0]](images/dmf_217.gif){kind=small}
![y1[0, 0] = -kappa[0, 0]](images/dmf_218.gif){kind=small}
![a[2, 0] = b[1, 1]+1/2*kappa[2, 0]+3/2*kappa[0, 0]*kappa[1, 0]-3/2*kappa[0, 0]^2*a[0, 0]+3*kappa[0, 0]*a[0, 0]^2-3/2*kappa[0, 0]*b[0, 1]-1/2*kappa[0, 2]-5/2*kappa[0, 1]*b[0, 0]-3*kappa[0, 0]*b[0, 0]^2+...](images/dmf_219.gif){kind=small}
![a[2, 0] = b[1, 1]+1/2*kappa[2, 0]+3/2*kappa[0, 0]*kappa[1, 0]-3/2*kappa[0, 0]^2*a[0, 0]+3*kappa[0, 0]*a[0, 0]^2-3/2*kappa[0, 0]*b[0, 1]-1/2*kappa[0, 2]-5/2*kappa[0, 1]*b[0, 0]-3*kappa[0, 0]*b[0, 0]^2+...](images/dmf_220.gif){kind=small}
![a[2, 0] = b[1, 1]+1/2*kappa[2, 0]+3/2*kappa[0, 0]*kappa[1, 0]-3/2*kappa[0, 0]^2*a[0, 0]+3*kappa[0, 0]*a[0, 0]^2-3/2*kappa[0, 0]*b[0, 1]-1/2*kappa[0, 2]-5/2*kappa[0, 1]*b[0, 0]-3*kappa[0, 0]*b[0, 0]^2+...](images/dmf_221.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_222.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_223.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_224.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_225.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_226.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_227.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_228.gif){kind=small}
![b[2, 0] = 1/3*(-3*kappa[2, 1]-18*b[0, 0]*kappa[0, 0]*a[0, 0]^2+11*kappa[0, 1]*b[0, 0]^2-18*a[0, 0]^2*kappa[0, 1]+6*kappa[0, 0]*b[0, 0]^3+10*a[1, 0]*kappa[0, 1]+kappa[0, 3]+36*b[0, 0]*kappa[0, 0]^2*a[0...](images/dmf_229.gif){kind=small}
![a[1, 1] = 6*kappa[0, 0]*a[0, 0]*b[0, 0]+3*kappa[0, 1]*a[0, 0]+3/2*kappa[0, 0]*kappa[0, 1]+3/2*kappa[0, 0]^2*b[0, 0]+3*a[0, 0]*a[0, 1]-kappa[1, 1]-2*kappa[1, 0]*b[0, 0]+2*b[0, 0]*b[0, 1]+b[0, 2]+b[0, 0...](images/dmf_230.gif){kind=small}
![a[1, 1] = 6*kappa[0, 0]*a[0, 0]*b[0, 0]+3*kappa[0, 1]*a[0, 0]+3/2*kappa[0, 0]*kappa[0, 1]+3/2*kappa[0, 0]^2*b[0, 0]+3*a[0, 0]*a[0, 1]-kappa[1, 1]-2*kappa[1, 0]*b[0, 0]+2*b[0, 0]*b[0, 1]+b[0, 2]+b[0, 0...](images/dmf_231.gif){kind=small}
![a[1, 1] = 6*kappa[0, 0]*a[0, 0]*b[0, 0]+3*kappa[0, 1]*a[0, 0]+3/2*kappa[0, 0]*kappa[0, 1]+3/2*kappa[0, 0]^2*b[0, 0]+3*a[0, 0]*a[0, 1]-kappa[1, 1]-2*kappa[1, 0]*b[0, 0]+2*b[0, 0]*b[0, 1]+b[0, 2]+b[0, 0...](images/dmf_232.gif){kind=small}
| fr > | R := differential_ring(ranking=[[y0,y1],[c,d,e],[S2,S1,Pk]], derivations=[x,y],
commutations=COM,notation=vjet); CC := Rosenfeld_Groebner(equations(C[1]), [Pk[0,0]], R); for g in rewrite_rules(CC[1]) do print(g); od; |
![(Typesetting:-mprintslash)([R := differential_polynomial_ring], [differential_polynomial_ring])](images/dmf_233.gif){kind=small}
![(Typesetting:-mprintslash)([CC := [characterisable]], [[characterisable]])](images/dmf_234.gif){kind=small}
![y0[0, 0] = 1/Pk[0, 0]](images/dmf_235.gif){kind=small}
![y1[0, 0] = -Pk[0, 0]](images/dmf_236.gif){kind=small}
![c[0, 0] = -1/2*Pk[1, 0]-S2[0, 0]^2-3/2*Pk[0, 0]*S2[0, 0]-S1[0, 0]^2-S1[0, 1]+S2[1, 0]](images/dmf_237.gif){kind=small}
![d[0, 0] = -1/2*Pk[0, 1]-9/2*Pk[0, 0]*S1[0, 0]](images/dmf_238.gif){kind=small}
![e[0, 0] = 5/2*Pk[1, 0]-3*S2[0, 0]^2-9/2*Pk[0, 0]*S2[0, 0]-3*S1[0, 0]^2-3*S1[0, 1]+3*S2[1, 0]](images/dmf_239.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_240.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_241.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_242.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_243.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_244.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_245.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_246.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_247.gif){kind=small}
![Pk[2, 1] = 1/3*Pk[0, 3]+8*Pk[0, 0]*S2[0, 0]*Pk[0, 1]+6*Pk[0, 0]*S1[0, 0]*S2[1, 0]+12*S1[0, 0]*Pk[0, 0]^2*S2[0, 0]-6*S1[0, 0]*Pk[0, 0]*S2[0, 0]^2+9*Pk[0, 0]*S1[0, 0]*S1[0, 1]+5*Pk[0, 0]*S1[1, 0]*S2[0, ...](images/dmf_248.gif){kind=small}
![S2[2, 0] = -5/2*Pk[1, 0]*S2[0, 0]-3/2*Pk[0, 0]^2*S2[0, 0]+3/2*Pk[0, 0]*Pk[1, 0]+3*Pk[0, 0]*S2[0, 0]^2-3*Pk[0, 0]*S1[0, 0]^2-3/2*Pk[0, 0]*S1[0, 1]-3/2*Pk[0, 0]*S2[1, 0]-5/2*Pk[0, 1]*S1[0, 0]-1/2*Pk[0, ...](images/dmf_249.gif){kind=small}
![S2[2, 0] = -5/2*Pk[1, 0]*S2[0, 0]-3/2*Pk[0, 0]^2*S2[0, 0]+3/2*Pk[0, 0]*Pk[1, 0]+3*Pk[0, 0]*S2[0, 0]^2-3*Pk[0, 0]*S1[0, 0]^2-3/2*Pk[0, 0]*S1[0, 1]-3/2*Pk[0, 0]*S2[1, 0]-5/2*Pk[0, 1]*S1[0, 0]-1/2*Pk[0, ...](images/dmf_250.gif){kind=small}
![S2[2, 0] = -5/2*Pk[1, 0]*S2[0, 0]-3/2*Pk[0, 0]^2*S2[0, 0]+3/2*Pk[0, 0]*Pk[1, 0]+3*Pk[0, 0]*S2[0, 0]^2-3*Pk[0, 0]*S1[0, 0]^2-3/2*Pk[0, 0]*S1[0, 1]-3/2*Pk[0, 0]*S2[1, 0]-5/2*Pk[0, 1]*S1[0, 0]-1/2*Pk[0, ...](images/dmf_251.gif){kind=small}
![S2[2, 0] = -5/2*Pk[1, 0]*S2[0, 0]-3/2*Pk[0, 0]^2*S2[0, 0]+3/2*Pk[0, 0]*Pk[1, 0]+3*Pk[0, 0]*S2[0, 0]^2-3*Pk[0, 0]*S1[0, 0]^2-3/2*Pk[0, 0]*S1[0, 1]-3/2*Pk[0, 0]*S2[1, 0]-5/2*Pk[0, 1]*S1[0, 0]-1/2*Pk[0, ...](images/dmf_252.gif){kind=small}
![S2[1, 1] = 3*Pk[0, 1]*S2[0, 0]+6*Pk[0, 0]*S1[0, 0]*S2[0, 0]+3/2*Pk[0, 0]*Pk[0, 1]+3/2*Pk[0, 0]^2*S1[0, 0]-Pk[1, 1]-2*Pk[1, 0]*S1[0, 0]+3*S2[0, 0]*S2[0, 1]+3/2*Pk[0, 0]*S2[0, 1]+2*S1[0, 0]*S1[0, 1]+S1[...](images/dmf_253.gif){kind=small}
![S2[1, 1] = 3*Pk[0, 1]*S2[0, 0]+6*Pk[0, 0]*S1[0, 0]*S2[0, 0]+3/2*Pk[0, 0]*Pk[0, 1]+3/2*Pk[0, 0]^2*S1[0, 0]-Pk[1, 1]-2*Pk[1, 0]*S1[0, 0]+3*S2[0, 0]*S2[0, 1]+3/2*Pk[0, 0]*S2[0, 1]+2*S1[0, 0]*S1[0, 1]+S1[...](images/dmf_254.gif){kind=small}
![S2[1, 1] = 3*Pk[0, 1]*S2[0, 0]+6*Pk[0, 0]*S1[0, 0]*S2[0, 0]+3/2*Pk[0, 0]*Pk[0, 1]+3/2*Pk[0, 0]^2*S1[0, 0]-Pk[1, 1]-2*Pk[1, 0]*S1[0, 0]+3*S2[0, 0]*S2[0, 1]+3/2*Pk[0, 0]*S2[0, 1]+2*S1[0, 0]*S1[0, 1]+S1[...](images/dmf_255.gif){kind=small}
![S2[1, 1] = 3*Pk[0, 1]*S2[0, 0]+6*Pk[0, 0]*S1[0, 0]*S2[0, 0]+3/2*Pk[0, 0]*Pk[0, 1]+3/2*Pk[0, 0]^2*S1[0, 0]-Pk[1, 1]-2*Pk[1, 0]*S1[0, 0]+3*S2[0, 0]*S2[0, 1]+3/2*Pk[0, 0]*S2[0, 1]+2*S1[0, 0]*S1[0, 1]+S1[...](images/dmf_256.gif){kind=small}