Abelian group G_P
from P. Olver, On generating Differential Invariants, in preparation.
| > | coord_frame([x,y],[u],fr): |
| fr > | P := [1,x,y,2*x*y-x^2,2*x*y-y^2,2*(x^3+y^3)-3*x*y*(x+y)]; |
![(Typesetting:-mprintslash)([P := [1, x, y, 2*x*y-x^2, 2*x*y-y^2, 2*x^3+2*y^3-3*x*y*(x+y)]], [[1, x, y, 2*x*y-x^2, 2*x*y-y^2, 2*x^3+2*y^3-3*x*y*(x+y)]])](images/dmf_257.gif){kind=small}
| fr > | LieAlg:=[[1,0,0],[0,1,0], seq([0,0,p],p=P)]:
LieAlg:=map( V-> v_zip(V,frameJetVariables(fr,0)[1..3],plus, vect), LieAlg); nops(LieAlg); |
![(Typesetting:-mprintslash)([LieAlg := [D_x[``], D_y[``], D_u[[0, 0]][``], x*D_u[[0, 0]][``], y*D_u[[0, 0]][``], (2*x*y-x^2)*D_u[[0, 0]][``], (2*x*y-y^2)*D_u[[0, 0]][``], (2*x^3+2*y^3-3*x^2*y-3*x*y^2)*...](images/dmf_258.gif){kind=small}
![(Typesetting:-mprintslash)([LieAlg := [D_x[``], D_y[``], D_u[[0, 0]][``], x*D_u[[0, 0]][``], y*D_u[[0, 0]][``], (2*x*y-x^2)*D_u[[0, 0]][``], (2*x*y-y^2)*D_u[[0, 0]][``], (2*x^3+2*y^3-3*x^2*y-3*x*y^2)*...](images/dmf_259.gif){kind=small}
![(Typesetting:-mprintslash)([LieAlg := [D_x[``], D_y[``], D_u[[0, 0]][``], x*D_u[[0, 0]][``], y*D_u[[0, 0]][``], (2*x*y-x^2)*D_u[[0, 0]][``], (2*x*y-y^2)*D_u[[0, 0]][``], (2*x^3+2*y^3-3*x^2*y-3*x*y^2)*...](images/dmf_260.gif){kind=small}
| fr > | Section:=[x=0,y=0,u[0,0]=0,u[1,0]=0,u[0,1]=0,u[2,0]=0,u[0,2]=0,u[3,0]=0]: stair(Section);
C, Morphism :=dmf(LieAlg,Section, fr, [op(Section), u[1,1]=a,u[3,0]=b,u[0,4]=c]): |
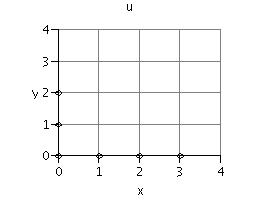
"Section :"
![[u[3, 0] = 0, u[0, 2] = 0, u[2, 0] = 0, u[0, 1] = 0, u[1, 0] = 0, u[0, 0] = 0, y = 0, x = 0]](images/dmf_263.gif){kind=small}
"Transversality condition :" 1
"Invariantizations:"
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[2, 0] = 0, u[0, 2] = 0, u[3, 0] = 0, u[1, 1] = a, u[3, 0] = b, u[0, 4] = c, u[2, 1] = y1, u[1, 2] = y2, u[0, 3] = y3, u[4, 0] = y4, u[3, 1] = y5,...](images/dmf_264.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[2, 0] = 0, u[0, 2] = 0, u[3, 0] = 0, u[1, 1] = a, u[3, 0] = b, u[0, 4] = c, u[2, 1] = y1, u[1, 2] = y2, u[0, 3] = y3, u[4, 0] = y4, u[3, 1] = y5,...](images/dmf_265.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[2, 0] = 0, u[0, 2] = 0, u[3, 0] = 0, u[1, 1] = a, u[3, 0] = b, u[0, 4] = c, u[2, 1] = y1, u[1, 2] = y2, u[0, 3] = y3, u[4, 0] = y4, u[3, 1] = y5,...](images/dmf_266.gif){kind=small}
"Commutation rules"
![[D1, D2] = 0](images/dmf_267.gif){kind=small}
"Syzygies"
![[-y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]+y4[0, 0]-y7[0, 0], 2*y2[1, 0]-y4[0, 0]-2*y6[0, 0], 2*y1[1, 0]-y4[0, 0]-2*y5[0, 0], a[1, 0]-y2[0, 0]-y1[0, 0], -y7[0, 1]+c[1, 0], y...](images/dmf_268.gif){kind=small}
![[-y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]+y4[0, 0]-y7[0, 0], 2*y2[1, 0]-y4[0, 0]-2*y6[0, 0], 2*y1[1, 0]-y4[0, 0]-2*y5[0, 0], a[1, 0]-y2[0, 0]-y1[0, 0], -y7[0, 1]+c[1, 0], y...](images/dmf_269.gif){kind=small}
![[-y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]+y4[0, 0]-y7[0, 0], 2*y2[1, 0]-y4[0, 0]-2*y6[0, 0], 2*y1[1, 0]-y4[0, 0]-2*y5[0, 0], a[1, 0]-y2[0, 0]-y1[0, 0], -y7[0, 1]+c[1, 0], y...](images/dmf_270.gif){kind=small}
![[-y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]+y4[0, 0]-y7[0, 0], 2*y2[1, 0]-y4[0, 0]-2*y6[0, 0], 2*y1[1, 0]-y4[0, 0]-2*y5[0, 0], a[1, 0]-y2[0, 0]-y1[0, 0], -y7[0, 1]+c[1, 0], y...](images/dmf_271.gif){kind=small}
![[-y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]+y4[0, 0]-y7[0, 0], 2*y2[1, 0]-y4[0, 0]-2*y6[0, 0], 2*y1[1, 0]-y4[0, 0]-2*y5[0, 0], a[1, 0]-y2[0, 0]-y1[0, 0], -y7[0, 1]+c[1, 0], y...](images/dmf_272.gif){kind=small}
"Syzygies with attempt to eliminate the y's"
![y0[0, 0] = 1](images/dmf_273.gif){kind=small}
![y4[1, 0] = a[0, 3]-c[0, 1]+a[3, 0]-a[2, 1]-c[1, 0]](images/dmf_274.gif){kind=small}
![y1[1, 0] = a[1, 1]+1/2*y4[0, 0]-a[0, 2]+c[0, 0]](images/dmf_275.gif){kind=small}
![y4[0, 1] = a[2, 1]-a[1, 2]+c[1, 0]](images/dmf_276.gif){kind=small}
![y1[0, 1] = -1/2*a[1, 1]+1/2*a[0, 2]-1/2*c[0, 0]+a[2, 0]-y4[0, 0]](images/dmf_277.gif){kind=small}
![y7[0, 0] = -a[2, 0]+a[1, 1]+y4[0, 0]](images/dmf_278.gif){kind=small}
![y6[0, 0] = a[2, 0]-a[1, 1]-y4[0, 0]+a[0, 2]-c[0, 0]](images/dmf_279.gif){kind=small}
![y5[0, 0] = a[1, 1]-a[0, 2]+c[0, 0]](images/dmf_280.gif){kind=small}
![y3[0, 0] = a[0, 1]-a[1, 0]](images/dmf_281.gif){kind=small}
![y2[0, 0] = a[1, 0]-y1[0, 0]](images/dmf_282.gif){kind=small}
![a[0, 4] = c[0, 2]+c[1, 1]+c[2, 0]](images/dmf_283.gif){kind=small}
| fr > | Section:=[x=0,y=0,u[0,0]=0,u[1,0]=0,u[0,1]=0,u[2,0]=0,u[1,1]=0,u[2,1]=0]: stair(Section);
C, Morphism :=dmf(LieAlg,Section, fr, [op(Section), u[2,0]=a,u[3,0]=b]): |
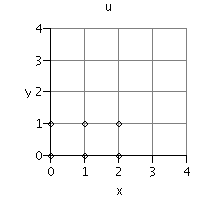
"Section :"
![[u[2, 1] = 0, u[1, 1] = 0, u[2, 0] = 0, u[0, 1] = 0, u[1, 0] = 0, u[0, 0] = 0, y = 0, x = 0]](images/dmf_285.gif){kind=small}
"Transversality condition :" 1
"Invariantizations:"
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[2, 0] = 0, u[1, 1] = 0, u[2, 1] = 0, u[2, 0] = a, u[3, 0] = b, u[0, 2] = y1, u[1, 2] = y2, u[0, 3] = y3, u[4, 0] = y4, u[3, 1] = y5, u[2, 2] = y6...](images/dmf_286.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[2, 0] = 0, u[1, 1] = 0, u[2, 1] = 0, u[2, 0] = a, u[3, 0] = b, u[0, 2] = y1, u[1, 2] = y2, u[0, 3] = y3, u[4, 0] = y4, u[3, 1] = y5, u[2, 2] = y6...](images/dmf_287.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[2, 0] = 0, u[1, 1] = 0, u[2, 1] = 0, u[2, 0] = a, u[3, 0] = b, u[0, 2] = y1, u[1, 2] = y2, u[0, 3] = y3, u[4, 0] = y4, u[3, 1] = y5, u[2, 2] = y6...](images/dmf_288.gif){kind=small}
"Commutation rules"
![[D1, D2] = 0](images/dmf_289.gif){kind=small}
"Syzygies"
![[-y7[0, 1]+y8[1, 0], -y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]-2*y5[0, 0]-y7[0, 0], y2[1, 0]+y5[0, 0]-y6[0, 0], y1[1, 0]-b[0, 0]-y2[0, 0], b[1, 0]-2*y5[0, 0]-y4[0, 0], y3[0,...](images/dmf_290.gif){kind=small}
![[-y7[0, 1]+y8[1, 0], -y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]-2*y5[0, 0]-y7[0, 0], y2[1, 0]+y5[0, 0]-y6[0, 0], y1[1, 0]-b[0, 0]-y2[0, 0], b[1, 0]-2*y5[0, 0]-y4[0, 0], y3[0,...](images/dmf_291.gif){kind=small}
![[-y7[0, 1]+y8[1, 0], -y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]-2*y5[0, 0]-y7[0, 0], y2[1, 0]+y5[0, 0]-y6[0, 0], y1[1, 0]-b[0, 0]-y2[0, 0], b[1, 0]-2*y5[0, 0]-y4[0, 0], y3[0,...](images/dmf_292.gif){kind=small}
![[-y7[0, 1]+y8[1, 0], -y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]-2*y5[0, 0]-y7[0, 0], y2[1, 0]+y5[0, 0]-y6[0, 0], y1[1, 0]-b[0, 0]-y2[0, 0], b[1, 0]-2*y5[0, 0]-y4[0, 0], y3[0,...](images/dmf_293.gif){kind=small}
![[-y7[0, 1]+y8[1, 0], -y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]-2*y5[0, 0]-y7[0, 0], y2[1, 0]+y5[0, 0]-y6[0, 0], y1[1, 0]-b[0, 0]-y2[0, 0], b[1, 0]-2*y5[0, 0]-y4[0, 0], y3[0,...](images/dmf_294.gif){kind=small}
![[-y7[0, 1]+y8[1, 0], -y6[0, 1]+y7[1, 0], -y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], y3[1, 0]-2*y5[0, 0]-y7[0, 0], y2[1, 0]+y5[0, 0]-y6[0, 0], y1[1, 0]-b[0, 0]-y2[0, 0], b[1, 0]-2*y5[0, 0]-y4[0, 0], y3[0,...](images/dmf_295.gif){kind=small}
"Syzygies with attempt to eliminate the y's"
![y0[0, 0] = 1](images/dmf_296.gif){kind=small}
![y8[1, 0] = y7[0, 1]](images/dmf_297.gif){kind=small}
![y7[1, 0] = 1/2*b[0, 2]+1/4*y4[0, 1]-1/4*b[1, 1]](images/dmf_298.gif){kind=small}
![y4[1, 0] = -2*y4[0, 1]+b[2, 0]](images/dmf_299.gif){kind=small}
![y3[1, 0] = b[1, 0]-y4[0, 0]+y7[0, 0]](images/dmf_300.gif){kind=small}
![y2[1, 0] = -3/4*b[1, 0]+3/4*y4[0, 0]+1/2*b[0, 1]](images/dmf_301.gif){kind=small}
![y1[1, 0] = b[0, 0]+y2[0, 0]](images/dmf_302.gif){kind=small}
![y3[0, 1] = b[0, 1]-1/2*b[1, 0]+1/2*y4[0, 0]+y8[0, 0]](images/dmf_303.gif){kind=small}
![y2[0, 1] = y7[0, 0]-1/2*b[0, 1]+1/4*b[1, 0]-1/4*y4[0, 0]](images/dmf_304.gif){kind=small}
![y1[0, 1] = y2[0, 0]+y3[0, 0]](images/dmf_305.gif){kind=small}
![y6[0, 0] = 1/2*b[0, 1]-1/4*b[1, 0]+1/4*y4[0, 0]](images/dmf_306.gif){kind=small}
![y5[0, 0] = 1/2*b[1, 0]-1/2*y4[0, 0]](images/dmf_307.gif){kind=small}
| fr > | Section:=[x=0,y=0,u[0,0]=0,u[1,0]=0,u[0,1]=0,u[0,2]=0,u[1,1]=0,u[0,3]=0]: stair(Section);
C, Morphism :=dmf(LieAlg,Section, fr, [op(Section), u[2,0]=a,u[1,2]=b,u[0,4]=c]): |
"Section :"
![[u[0, 3] = 0, u[0, 2] = 0, u[1, 1] = 0, u[0, 1] = 0, u[1, 0] = 0, u[0, 0] = 0, y = 0, x = 0]](images/dmf_309.gif){kind=small}
"Transversality condition :" -1
"Invariantizations:"
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[0, 2] = 0, u[1, 1] = 0, u[0, 3] = 0, u[2, 0] = a, u[1, 2] = b, u[0, 4] = c, u[3, 0] = y1, u[2, 1] = y2, u[4, 0] = y3, u[3, 1] = y4, u[2, 2] = y5,...](images/dmf_310.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[0, 2] = 0, u[1, 1] = 0, u[0, 3] = 0, u[2, 0] = a, u[1, 2] = b, u[0, 4] = c, u[3, 0] = y1, u[2, 1] = y2, u[4, 0] = y3, u[3, 1] = y4, u[2, 2] = y5,...](images/dmf_311.gif){kind=small}
![x = 0, y = 0, u[0, 0] = 0, u[1, 0] = 0, u[0, 1] = 0, u[0, 2] = 0, u[1, 1] = 0, u[0, 3] = 0, u[2, 0] = a, u[1, 2] = b, u[0, 4] = c, u[3, 0] = y1, u[2, 1] = y2, u[4, 0] = y3, u[3, 1] = y4, u[2, 2] = y5,...](images/dmf_312.gif){kind=small}
"Commutation rules"
![[D1, D2] = 0](images/dmf_313.gif){kind=small}
"Syzygies"
![[-y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], -y3[0, 1]+y4[1, 0], 2*y2[1, 0]-y6[0, 0]-2*y4[0, 0], y1[1, 0]+y6[0, 0]-y3[0, 0], a[1, 0]-b[0, 0]-y2[0, 0]-y1[0, 0], -y6[0, 1]+c[1, 0], 2*b[1, 0]-y6[0, 0]-2*y5[0...](images/dmf_314.gif){kind=small}
![[-y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], -y3[0, 1]+y4[1, 0], 2*y2[1, 0]-y6[0, 0]-2*y4[0, 0], y1[1, 0]+y6[0, 0]-y3[0, 0], a[1, 0]-b[0, 0]-y2[0, 0]-y1[0, 0], -y6[0, 1]+c[1, 0], 2*b[1, 0]-y6[0, 0]-2*y5[0...](images/dmf_315.gif){kind=small}
![[-y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], -y3[0, 1]+y4[1, 0], 2*y2[1, 0]-y6[0, 0]-2*y4[0, 0], y1[1, 0]+y6[0, 0]-y3[0, 0], a[1, 0]-b[0, 0]-y2[0, 0]-y1[0, 0], -y6[0, 1]+c[1, 0], 2*b[1, 0]-y6[0, 0]-2*y5[0...](images/dmf_316.gif){kind=small}
![[-y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], -y3[0, 1]+y4[1, 0], 2*y2[1, 0]-y6[0, 0]-2*y4[0, 0], y1[1, 0]+y6[0, 0]-y3[0, 0], a[1, 0]-b[0, 0]-y2[0, 0]-y1[0, 0], -y6[0, 1]+c[1, 0], 2*b[1, 0]-y6[0, 0]-2*y5[0...](images/dmf_317.gif){kind=small}
![[-y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], -y3[0, 1]+y4[1, 0], 2*y2[1, 0]-y6[0, 0]-2*y4[0, 0], y1[1, 0]+y6[0, 0]-y3[0, 0], a[1, 0]-b[0, 0]-y2[0, 0]-y1[0, 0], -y6[0, 1]+c[1, 0], 2*b[1, 0]-y6[0, 0]-2*y5[0...](images/dmf_318.gif){kind=small}
![[-y5[0, 1]+y6[1, 0], -y4[0, 1]+y5[1, 0], -y3[0, 1]+y4[1, 0], 2*y2[1, 0]-y6[0, 0]-2*y4[0, 0], y1[1, 0]+y6[0, 0]-y3[0, 0], a[1, 0]-b[0, 0]-y2[0, 0]-y1[0, 0], -y6[0, 1]+c[1, 0], 2*b[1, 0]-y6[0, 0]-2*y5[0...](images/dmf_319.gif){kind=small}
"Syzygies with attempt to eliminate the y's"
![y0[0, 0] = -1](images/dmf_320.gif){kind=small}
![y6[0, 0] = b[0, 1]-1/2*c[0, 0]](images/dmf_321.gif){kind=small}
![y5[0, 0] = -1/2*b[0, 1]+1/4*c[0, 0]+b[1, 0]](images/dmf_322.gif){kind=small}
![y4[0, 0] = a[1, 1]-1/2*b[0, 1]+1/4*c[0, 0]-b[1, 0]](images/dmf_323.gif){kind=small}
![y3[0, 0] = -a[1, 1]+b[0, 1]-1/2*c[0, 0]+a[2, 0]](images/dmf_324.gif){kind=small}
![y2[0, 0] = a[0, 1]-b[0, 0]](images/dmf_325.gif){kind=small}
![y1[0, 0] = -a[0, 1]+a[1, 0]](images/dmf_326.gif){kind=small}
![a[0, 2] = 1/2*b[0, 1]+3/4*c[0, 0]+b[1, 0]](images/dmf_327.gif){kind=small}
![b[0, 2] = 1/2*c[0, 1]+c[1, 0]](images/dmf_328.gif){kind=small}