|
1.Paramétrisation et equation implicite d'une courbe
Voici un exemple d'utilisation de Macaulay 2. Les données peuvent être modifiées et les calculs relancés.
Soit 
la courbe du plan
paramétrée par
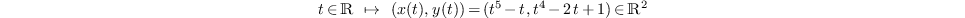
Calculer une équation implicite de ,
c'est-à-dire un polynôme 
de plus
petit degré tel que 
pour tout 
.
Macaulay 2, version 1.1
with packages: Classic, Core, Elimination,
IntegralClosure, LLLBases, Parsing,
PrimaryDecomposition, SchurRings, TangentCone
i1 :
R = QQ[t,x,y, MonomialOrder=>Eliminate 1]
i2 :
I = ideal (x-t^5+t,y-t^4+2*t-1)
i3 :
gb I
i4 :
L = entries gens gb I
i5 :
L#0#0
i22 :
2.Une surface paramétrée
Soit 
la surface paramétrée par
Calculer une équation implicite de ,
c'est-à-dire un polynôme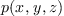 
de plus
petit degré tel que 
pour tout 
.
Même question pour la paramétrisation
Macaulay2, version 1.7
with packages: ConwayPolynomials, Elimination,
IntegralClosure, LLLBases,
PrimaryDecomposition, ReesAlgebra, TangentCone
i1 :
R = QQ[u,v, x,y,z, MonomialOrder=>Eliminate 2 ]
i2 :
I = ideal ( (1+u^3+v^3)*x-(1-u^3-v^2),
(1+u^3+v^3)*y-(2*u^3-v^2*u), (1+u^3+v^3)*z-2*v)
i4 :
L = entries gens gb I; L#0#0
i4 :
L#0#0
i6 :
I = ideal ( (1+u^3+v^3)*x-(1-u^2-v^2),
(1+u^3+v^3)*y-(v^2*u+u+1), (1+u^3+v^3)*z-2*v)
i7 :
L = entries gens gb I; L#0#0
i9 :
J = saturate (I, ideal(1+u^3+v^3));
i10 :
L = entries gens gb J; L#0#0
i10 :
3.Exercices
En s'inspirant des calculs ci-dessus:
-
Trouver les équations vérifiées par un point
de la courbe paramétrée par
(c'est-à-dire tel que
)
-
Même question pour la courbe paramétrée par
-
Calculer un système générateur du module des syzygies de
-
Vérifier que l'on obtient une matrice
dont les mineurs 
sont les polynômes
ci-dessus (à un scalaire près).
-
Cette propriété reste-t-elle vraie pour
Répondre sous forme d'une session de calculs avec Macaulay2 (comme dans la section précédente).