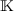un corps, 
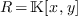et 
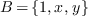. Soit 
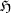l'ensemble des
algèbres quotients 
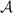de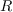 
par un idéal 
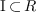, ayant pour base 
.
|
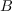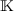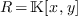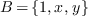Soit un corps, et . Soit 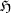l'ensemble des
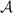algèbres quotients de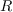
par un idéal 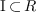, ayant pour base .
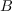En introduisant des variables pour les coefficients des formes
normales de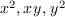 
, calculer les matrices de
multiplication par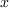 
et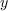 
dans la base B d'une algèbre quotient de .
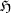En utilisant la caractérisation des bases de bord, calculer
les équations de 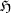dans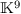 
.
Quelle est la dimension et le degré de ?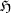
Soit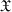 
l'ensemble des algèbres
quotients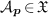 
par les idéaux des
polynômes qui s'annullent en 3 points génériques
, 
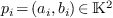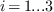de .
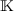On note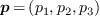 
. Montrer que
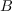est une base de ces algèbres.
Montrer que les polynômes suivants s'anullent dans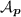 
:
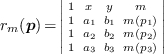
où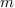 
est un polynôme de R.
En déduire la forme normale de tout polynôme dans la
bas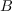e de 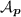en fonction
de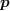 
.
Donner une description de la base de bord de B associée
à 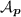en fonction de
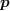et une paramétrisation de l'ensemble des algèbre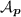s dans .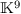
Décrire une base du dual de 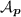en
fonction de .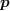
En utilisant un ordre d'élimination, calculer les équations implicites de la cloture de Zariski de l'image de cette paramétrisation, sa dimension et son degré.
Comparer 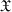et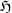 
. En
déduire que ℌB est une
variété irréductible de .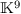
Fonctions utiles de Macaulay2: matrix, transpose, *, entries, flatten, dim, degree, eliminate, Matrix | Matrix, minors, flattenRing, saturate.
Macaulay2, version 1.7
with packages: ConwayPolynomials, Elimination, IntegralClosure, LLLBases,
PrimaryDecomposition,
ReesAlgebra, TangentCone
i1 :
R = ZZ/32051[c_1..c_9]
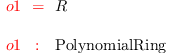
i2 :
B = {1,x,y}
i3 :
Ms = transpose (matrix {{0,1,0},{c_1,c_2,c_3},
{c_4,c_5,c_6}})
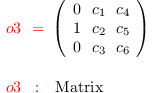
i4 :
Mt = transpose (matrix {{0,0,1},{c_4,c_5,c_6},
{c_7,c_8,c_9}})
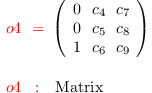
i5 :
C = Ms*Mt-Mt*Ms
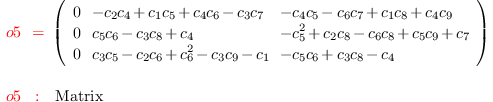
i6 :
I = ideal(flatten entries C)
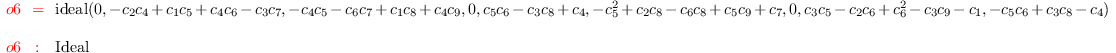
i7 :
dim I
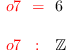
i8 :
degree I
i9 :
isPrime I
i10 :
Rxy = ZZ/32051[a_1..a_3,b_1..b_3,c_1..c_9][x,y]
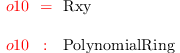
i11 :
r1 = det (matrix ({{x^2, 1,x,y}, {a_1^2,
1,a_1,b_1},{a_2^2,1,a_2,b_2},{a_3^2,1,a_3,b_3}}))
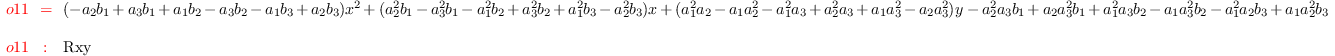
i12 :
r2 = det (matrix ({{x*y, 1,x,y}, {a_1*b_1,
1,a_1,b_1},{a_2*b_2,1,a_2,b_2},{a_3*b_3,1,a_3,b_3}}))
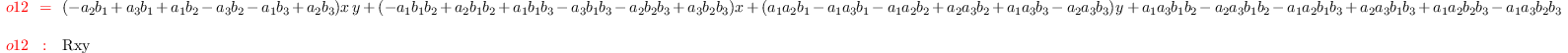
i13 :
r3 = det (matrix ({{y^2, 1,x,y}, {b_1^2,
1,a_1,b_1},{b_2^2,1,a_2,b_2},{b_3^2,1,a_3,b_3}}))
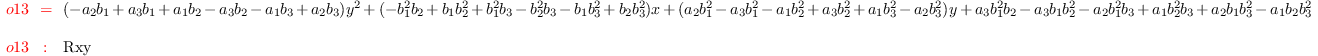
i16 :
D = ideal ((coefficients( r1, Monomials=> {x^2}))#1)
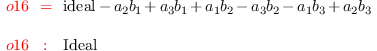
i17 :
C1 = matrix {{c_1},{c_2},{c_3},{1}}
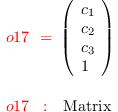
i29 :
M1 = minors(2,(coefficients( r1, Monomials=>
{1,x,y,x^2}))#1|C1)
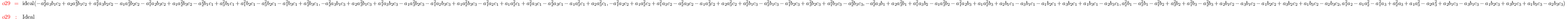
i30 :
i30 :
C2 = matrix {{c_4},{c_5},{c_6},{1}}
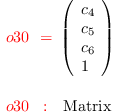
i31 :
M2 = minors(2,(coefficients( r2, Monomials=>
{1,x,y,x*y}))#1|C2)
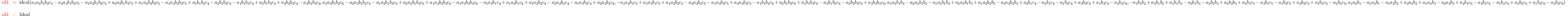
i32 :
i32 :
C3 = matrix {{c_7},{c_8},{c_9},{1}}
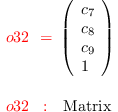
i33 :
M3 = minors(2,(coefficients( r3, Monomials=>
{1,x,y,y^2}))#1|C3)
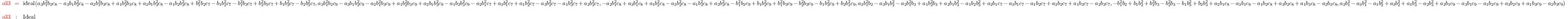
i34 :
(R,F) = flattenRing Rxy
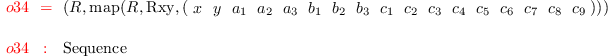
i35 :
J = M1+M2+M3
i36 :
K = F(J)
i37 :
E = F(D)
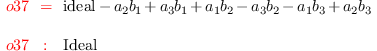
i41 :
codim K
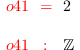
i42 :
degree K
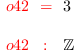
i43 :
G = saturate(K,E)
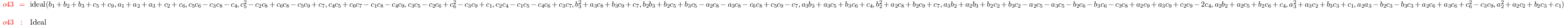
i45 :
codim G
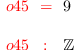
i46 :
G1 = eliminate({a_1,a_2,a_3,b_1,b_2,b_3}, G)
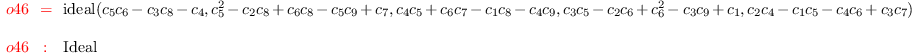
i47 :
codim G1
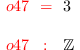
i48 :
degree G1
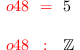
i49 :
isPrime G1
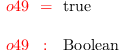
i50 :