On the Design of Virtual Networks (Sébastien Choplin)

Abstract:

The advent of fiber optic media has dramatically changed the classical views on the role and structure of digital communication networks. Specifically, the sharp distinction between telephone networks, cable television networks, and computer networks, has been replaced by a unified approach. Several communication schemes are achieved on virtual topologies designed on physical networks (ATM,MPCFS,WDM,...). In this context, we investigate the problem of designing such topologies, which consists of finding a set of paths satisfying some constraints in terms of load (the number of paths sharing a physical link) and hop count (the number of paths used to satisfy a connection). This problem has been studied in ATM context ([7],[4]) but can also be applied to more general communication scheme. This problem is an extension of the edge forwarding index problem ([5],[6],[3]) (where the hop count is one).

Model

We model the physical network by a graph G(V,E) where V is the set of nodes/vertices and E is the set of edges/links. We define a virtual graph H=(V,E') with the same set of vertices as G and a routing function P which associates a path P(e') in G to each edge e' in E' .

Load

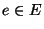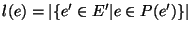Given a virtual graph H and a routing function P, the loadl(e) of an edge $e \in E$ of the physical graph is the number of paths that contain e; namely, $l(e)=\left\vert \left\{e' \in E' \verte\in P(e')\right\} \right\vert$ .
Given a H and P, the maximal edge load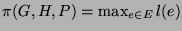 $\pi(G,H,P)=\max_{e\in E}l(e)$ .
Given a graph H, we are looking for a routing function P which minimizes 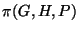$\pi(G,H,P)$ .
The minimal load of G for H is 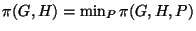$\pi(G,H)=\min_{P}\pi(G,H,P)$ .

Hop count

Given a set of requests I, the hop count of a request is the number of virtual links used to achieved this request and the maximum hop count is the maximum of the hop counts over all the requests.

Problems

Given a graph G and a set of requests, the following problems can be studied :

Given a hop count h , find H and P such that the maximal load is minimized
Given a maximum load, find H and P such that the maximum hop count is minimized

In the case of All-to-All set of requests and hop count 1, the problem which consists in finding P in order to minimize the load is the edge-forwarding index problem ([5],[6],[3]) (in this case, H is the complete graph).

Talk

After giving results on complexity of these problems on general graphs, we will study particular networks: paths and cycles. For a All-to-All set of requests, we give tight bounds on the network capacity (the maximum load of a physical link) as a function of the maximum hop count for each connection. These results can be found in [2] and [1].

References

1: Sébastien Choplin.
2: Sébastien Choplin.
3: F. R. K. Chung, E. G. Coffman, M. I. Reiman, and B. Simon.
4: Nausica Marlin.
5: J-C. Meyer, M-C. Heydemann, and D. Sotteau.
6: R. Saad.
7: S. Zaks.